题目内容
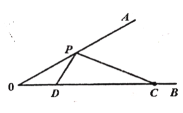
【题目】如图,在![]() 中,
中,![]() ,
,![]() 为线段
为线段![]() 的延长线上一点,且
的延长线上一点,且![]() ,
,![]() 于点
于点![]() ,取
,取![]() 的中点
的中点![]() ,连接
,连接![]() .
.
(1)求证:![]() ;
;
(2)若![]() ,求证:
,求证:![]() ;
;
【答案】(1)证明见解析;(2)证明见解析.
【解析】
(1)根据等腰三角形的性质和三角形内角和定理证明∠D=∠BAC,然后根据直角三角形两锐角互余即可证明;
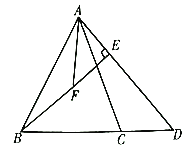
(2))如图,延长AF至M点,使AF=MF,连接BM,首先证明△AEF≌△MBF,可得AE=MB,再证明△ABM≌△ACD,可得MB=CD,由此即可证明.
(1)证明:∵![]()
∴∠ABC=∠ACB,∠BAC=180°-∠ABC-∠ACB=180°-2∠ABC,
∵![]()
∴∠ABC=∠BAD,∠D=180°-∠ABC-∠BAD=180°-2∠ABC,
∴∠BAC=∠D,
∵![]() ,
,
∴![]()
∴![]() ;
;
(2)证明:如图,延长AF至M点,使AF=MF,连接BM,

在△AEF和△MBF中
∵
∴△AEF≌△MBF(SAS),
∴AE=BM,∠DAF=∠FMB,
∵∠BAC=∠D,![]()
∴∠1=∠2,∠FMB=∠D,
在△ABM和△ACD中
∵
∴△ABM≌△ACD(AAS),
∴BM=CD,
∴AE=CD.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目