题目内容
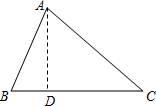 如图,△ABC是小新家的门口的一块空地,三边的长分别是AB=13米,BC=14米,AC=15米,现准备以每平方米50元的单价请承包商种植草皮,问共需要多少费用?
如图,△ABC是小新家的门口的一块空地,三边的长分别是AB=13米,BC=14米,AC=15米,现准备以每平方米50元的单价请承包商种植草皮,问共需要多少费用?分析:分析:欲知费用,只须算出△ABC的面积.由三角形面积公式可知应先求高,因此,选择以BC为底边,作高AD,设BD=x米,则DC=(14-x)米,在Rt△ABD与Rt△ACD中,由勾股定理,得:AB2-BD2=AD2=AC2-DC2,故132-x2=152-(14-x)2,求出x的值,在Rt△ABD中利用勾股定理可求出AD的长,故可得出△ABC的面积,由此即可得出结论.
解答:解:过点A作AD⊥BC,设BD=x米,则DC=(14-x)米,
∵在Rt△ABD与Rt△ACD中,由勾股定理得:AB2-BD2=AD2=AC2-DC2,即132-x2=152-(14-x)2,解得x=5,
∴AD=
=12,
∴S△ABC=
BC•AD=
×14×12=84(平方米),
∴共需要费用50×84=4200(元).
答:共需要4200元.
∵在Rt△ABD与Rt△ACD中,由勾股定理得:AB2-BD2=AD2=AC2-DC2,即132-x2=152-(14-x)2,解得x=5,
∴AD=
| 132-52 |
∴S△ABC=
| 1 |
| 2 |
| 1 |
| 2 |
∴共需要费用50×84=4200(元).
答:共需要4200元.
点评:本题考查的是勾股定理的应用,根据题意作出辅助线,构造出直角三角形,利用勾股定理求解是解答此题的关键.

练习册系列答案
 华东师大版一课一练系列答案
华东师大版一课一练系列答案 孟建平名校考卷系列答案
孟建平名校考卷系列答案
相关题目
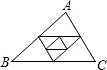 如图,△ABC的三条中位线组成一个新三角形,这个新三角形的三条中位线又组成一个小三角形,则这个小三角形的周长是原△ABC周长的( )
如图,△ABC的三条中位线组成一个新三角形,这个新三角形的三条中位线又组成一个小三角形,则这个小三角形的周长是原△ABC周长的( )A、
| ||
B、
| ||
C、
| ||
D、
|
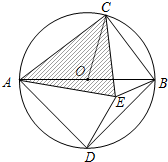 若在⊙O内存在点E,使AE=AD,CB=CE.
若在⊙O内存在点E,使AE=AD,CB=CE. 在如图中,每个小正方形的边长都是1,先把△ABC向右平移6个小方格,再绕点A的对应点逆时针方向旋转90度得到一个新的三角形.画出平移和旋转后的图形,标明对应字母.
在如图中,每个小正方形的边长都是1,先把△ABC向右平移6个小方格,再绕点A的对应点逆时针方向旋转90度得到一个新的三角形.画出平移和旋转后的图形,标明对应字母.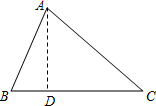 如图,△ABC是小新家的门口的一块空地,三边的长分别是AB=13米,BC=14米,AC=15米,现准备以每平方米50元的单价请承包商种植草皮,问共需要多少费用?
如图,△ABC是小新家的门口的一块空地,三边的长分别是AB=13米,BC=14米,AC=15米,现准备以每平方米50元的单价请承包商种植草皮,问共需要多少费用?