��Ŀ����
�����¶���һ�������Σ�����ƽ���͵��ڵ�����ƽ���������������ν������������Σ�
��1�����ݡ����������Ρ��Ķ��壬С��������⡰�ȱ�������һ�������������Ρ���������Ǽ����⣿
��2����Rt��ABC�У���C=90�㣬AB=c��AC=b��BC=a��b��a����Rt��ABC�����������Σ���a��b��c��
��3����ͼ��AB�ǡ�O��ֱ����C�ǡ�O��һ�㣨�����A��B�غϣ���D�ǰ�Բ���е㣬C��D��ֱ��AB�����࣬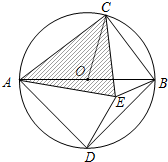 ���ڡ�O�ڴ��ڵ�E��ʹAE=AD��CB=CE��
���ڡ�O�ڴ��ڵ�E��ʹAE=AD��CB=CE��
����֤����ACE�����������Σ�
�ڵ���ACE��ֱ��������ʱ�����AOC�Ķ�����
��1�����ݡ����������Ρ��Ķ��壬С��������⡰�ȱ�������һ�������������Ρ���������Ǽ����⣿
��2����Rt��ABC�У���C=90�㣬AB=c��AC=b��BC=a��b��a����Rt��ABC�����������Σ���a��b��c��
��3����ͼ��AB�ǡ�O��ֱ����C�ǡ�O��һ�㣨�����A��B�غϣ���D�ǰ�Բ���е㣬C��D��ֱ��AB�����࣬
 ���ڡ�O�ڴ��ڵ�E��ʹAE=AD��CB=CE��
���ڡ�O�ڴ��ڵ�E��ʹAE=AD��CB=CE������֤����ACE�����������Σ�
�ڵ���ACE��ֱ��������ʱ�����AOC�Ķ�����
������1�����ݡ����������Ρ��Ķ�����ȱ������ε����ʣ���֤���ɣ�
��2�����ݹ��ɶ��������������ε����ʣ��ɵ�a2+b2=c2��a2+c2=2b2����a��ʾ��b��c��������ô𰸣�
��3����AB�ǡ�O��ֱ����������á�ACB=��ADB=90�㣬Ȼ�����ù��ɶ�����Բ�����ʼ���֤�ã�
�����ã�2���еĽ��ۣ��ֱ��AC��AE��CE=1��
��
��AC��AE��CE=
��
��1ȥ������������ý����
��2�����ݹ��ɶ��������������ε����ʣ��ɵ�a2+b2=c2��a2+c2=2b2����a��ʾ��b��c��������ô𰸣�
��3����AB�ǡ�O��ֱ����������á�ACB=��ADB=90�㣬Ȼ�����ù��ɶ�����Բ�����ʼ���֤�ã�
�����ã�2���еĽ��ۣ��ֱ��AC��AE��CE=1��
| 2 |
| 3 |
| 3 |
| 2 |
����⣺��1����ȱ������ε�һ��Ϊa����a2+a2=2a2��
��������������Ρ��Ķ��壮
����ȷ��
��2���ߡ�C=90�㣬
��a2+b2=c2�٣�
��Rt��ABC��������������b��a��
��a2+c2=2b2�ڣ�
�ɢ٢ڵã�b=
a��c=
a��
��a��b��c=1��
��
��
��3���١���ABΪб�߷ֱ���AB��������ֱ�������Σ�
����ֱ�����������Բֱ������б�ߣ�
��AB�ǡ�O��ֱ����
���ACB=��ADB=90�㣬
��Rt��ACB��AC2+BC2=AB2��
��Rt��ADB��AD2+BD2=AB2��
�ߵ�D�ǰ�Բ
���е㣬
��
=
��
��AD=BD��
��AB2=AD2+BD2=2AD2��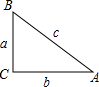
��AC2+CB2=2AD2��
�֡�CB=CE��AE=AD��
��AC2+CE2=2AE2��
���ACE������������
���ɢٿɵá�ACE�����������Σ�
��AC2+CE2=2AE2��
����ACE��ֱ��������ʱ��
�ɣ�2���ã�AC��AE��CE=1��
��
��AC��AE��CE=
��
��1��
��AC��AE��CE=1��
��
ʱ��AC��CE=1��
����AC��CB=1��
��
�ߡ�ACB=90�㣬
���ABC=30�㣬
���AOC=60��
��AC��AE��CE=
��
��1ʱ��AC��CE=
��1����AC��CB=
��1��
�ߡ�ACB=90�㣬
���ABC=60�㣬
���A0C=120�㣬
���Ͽ�֪����AOC=60���120�㣮
��������������Ρ��Ķ��壮
����ȷ��
��2���ߡ�C=90�㣬
��a2+b2=c2�٣�
��Rt��ABC��������������b��a��
��a2+c2=2b2�ڣ�
�ɢ٢ڵã�b=
| 2 |
| 3 |
��a��b��c=1��
| 2 |
| 3 |
��3���١���ABΪб�߷ֱ���AB��������ֱ�������Σ�
����ֱ�����������Բֱ������б�ߣ�
��AB�ǡ�O��ֱ����
���ACB=��ADB=90�㣬
��Rt��ACB��AC2+BC2=AB2��
��Rt��ADB��AD2+BD2=AB2��
�ߵ�D�ǰ�Բ
 |
| ADB |
��
 |
| AD |
 |
| BD |
��AD=BD��
��AB2=AD2+BD2=2AD2��

��AC2+CB2=2AD2��
�֡�CB=CE��AE=AD��
��AC2+CE2=2AE2��
���ACE������������
���ɢٿɵá�ACE�����������Σ�
��AC2+CE2=2AE2��

����ACE��ֱ��������ʱ��
�ɣ�2���ã�AC��AE��CE=1��
| 2 |
| 3 |
| 3 |
| 2 |
��AC��AE��CE=1��
| 2 |
| 3 |
| 3 |
| 3 |
�ߡ�ACB=90�㣬
���ABC=30�㣬
���AOC=60��
��AC��AE��CE=
| 3 |
| 2 |
| 3 |
| 3 |
�ߡ�ACB=90�㣬
���ABC=60�㣬
���A0C=120�㣬
���Ͽ�֪����AOC=60���120�㣮
���������⿼�����¶����֪ʶ�����ɶ����Լ�Բ�����ʣ����Ǻ�����֪ʶ������Ĺؼ����������⣬ץס���ν��˼���Ӧ�ã�

��ϰ��ϵ�д�
�����Ŀ
 �����¶���һ�������Σ�����ƽ���͵��ڵ�����ƽ����2���������ν������������Σ�
�����¶���һ�������Σ�����ƽ���͵��ڵ�����ƽ����2���������ν������������Σ�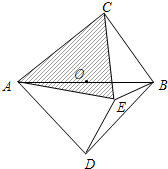 �Ķ�������龰�Ի���Ȼ�������⣺
�Ķ�������龰�Ի���Ȼ�������⣺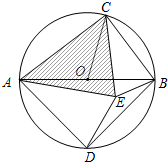 ���ڡ�O�ڴ��ڵ�E��ʹAE=AD��CB=CE��
���ڡ�O�ڴ��ڵ�E��ʹAE=AD��CB=CE��