Question

在四边形ABCD中，∠B=∠C=120°，AB=3，BC=4，CD=5，则此四边形的面积是________．

Answer 1

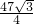
分析：延长BC，CB 分别作AE⊥EF，DF⊥EF，得梯形AEFD，解△ABE得BE，AE，解△CDF得CF，DF，根据四边形ABCD的面积为梯形AEFD的面积减去△ABE的面积减去△CDF的面积可以求解．
解答：解：延长BC，CB，作AE⊥EF，DF⊥EF，
∵∠B=∠C=120°，
∴∠EBA=∠FCD=60°，
∵AE⊥EF，FD⊥EF，
∴BE=AB=，CF=CD=，
AE=AB=，FD=CD=，
EF=EB+BC+CF=+4=8，
△ABE的面积为×AE×EB=，
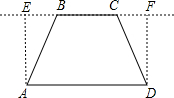
△CDF的面积为×CF×FD=，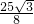
梯形AEFD的面积=（AE+DF）×EF=16，
∴四边形ABCD的面积为16--=．
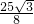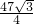故答案为．
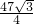点评：本题考查了勾股定理在直角三角形中的运用，考查了三角形、梯形面积的计算，本题中构造梯形AEFD是解题的关键．