Question

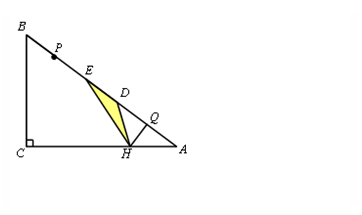
如图，Rt△ABC中，∠C=90°，BC=6，AC=8．点P，Q都是斜边AB上的动点，点P从B 向A运动（不与点B重合），点Q从A向B运动，BP=AQ．点D，E分别是点A，B以Q，P为对称中心的对称点， HQ⊥AB于Q，交AC于点H．当点E到达顶点A时，P，Q同时停止运动．设BP的长为x，△HDE的面积为y．
【小题1】求证：△DHQ∽△ABC；
【小题2】求y关于x的函数解析式并求y的最大值；
【小题3】当x为何值时，△HDE为等腰三角形？

Answer 1

【小题1】∵A、D关于点Q成中心对称，HQ⊥AB，
∴=90°，HD=HA，
∴，
∴△DHQ∽△ABC．
【小题1】①如图1，当时，
ED=，QH=，
此时．
当时，最大值．
②如图2，当时，
ED=，QH=，
此时．
当时，最大值．
∴y与x之间的函数解析式为
y的最大值是．

【小题1】①如图1，当时，
若DE=DH，∵DH=AH=， DE=，
∴=，．
显然ED=EH，HD=HE不可能；
②如图2，当时，
若DE=DH，=，；
若HD=HE，此时点D，E分别与点B，A重合，；
若ED=EH，则△EDH∽△HDA，
∴，，． 
∴当x的值为时，△HDE是等腰三角形解析:

【小题1】由两个对应角相等，满足了两个三角形相似的条件。
【小题1】根据函数解析式可以求得函数最大值。