题目内容
如图，已知在平行四边形ABCD中，M、N分别是边AD、DC的中点，设
，
．（1）求向量
（用向量
表示）；（2）求作向量
在
方向上的分向量．（不要求写作法，但要指出所作图中表示结论的向量）
【答案】分析：（1）根据线段的中点定义可得MD=
AD，DN=
AB，然后表示出
，
，再根据三角形法则求出
即可；
（2）以点M为圆心，以DN长为半径画弧，以点N为圆心，以MD长为半径画弧，交点为E，再根据平行四边形法则解答即可．
解答：解：（1）∵M、N分别是边AD、DC的中点，
∴MD=
AD，DN=
AB，
∵
=
，
=
，
∴
=
，
=
，
=
+
=
+
；
（2）如图所示，
为
在
方向上的向量，
为
在
方向上的向量．
点评：本题考查了平面向量的知识，平行四边形对边互相平行，线段中点的定义，向量的问题，熟练掌握三角形法则与平行四边形法则是解题的关键．
AD，DN=AB，然后表示出，，再根据三角形法则求出即可；（2）以点M为圆心，以DN长为半径画弧，以点N为圆心，以MD长为半径画弧，交点为E，再根据平行四边形法则解答即可．
解答：解：（1）∵M、N分别是边AD、DC的中点，
∴MD=
AD，DN=AB，∵
=，=，∴
=，=，=+=+；（2）如图所示，
为在方向上的向量，为在方向上的向量．点评：本题考查了平面向量的知识，平行四边形对边互相平行，线段中点的定义，向量的问题，熟练掌握三角形法则与平行四边形法则是解题的关键．
练习册系列答案
相关题目
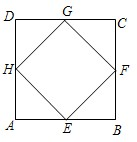四个顶点都在正方形边上的四边形叫做正方形的内接四边形．如图，四边形EFGH是正方形ABCD的内接平行四边形，且已知正方形ABCD的边长为4．
，BO＝AO．又∵AG⊥EB，∠1＋∠3＝
＝∠2＋∠3∴∠1＝∠2，∴Rt△BOE≌Rt△AOF解答此题后某同学产生了如下猜想：对上述命题，若点E在AC的延长线上，AG⊥EB，AG交EB的延长线于G，AG的延长线交DB的延长线于F，其它条件不变，如图，则仍有OE＝OF．问猜想所得的结论是否成立，请说明理由．
