题目内容
 如图,若梯形ABCD的两条对角线与两底所围成的两个三角形的面积为4和9,则梯形的面积为________.
如图,若梯形ABCD的两条对角线与两底所围成的两个三角形的面积为4和9,则梯形的面积为________.
25
分析:设AC与BD交于点O.先由AB∥CD,得出△COD∽△AOB,根据相似三角形的面积比等于相似比的平方得到 =(
=( )2=
)2= ,则
,则 =
= ,再根据等高不等底的两个三角形的面积比等于其对应底边的比得出
,再根据等高不等底的两个三角形的面积比等于其对应底边的比得出 =
= ,
, =
= ,求出S△AOD=S△COB=6,然后根据梯形ABCD的面积=S△AOD+S△AOB+S△COB+S△COD即可求解.
,求出S△AOD=S△COB=6,然后根据梯形ABCD的面积=S△AOD+S△AOB+S△COB+S△COD即可求解.
解答: 解:设AC与BD交于点O.
解:设AC与BD交于点O.
∵AB∥CD,
∴△COD∽△AOB,
∴ =(
=( )2=
)2= ,
,
∴ =
= .
.
∵ =
= ,
, =
= ,
,
∴S△AOD= S△AOB=
S△AOB= ×9=6,S△COB=
×9=6,S△COB= S△COD=
S△COD= ×4=6,
×4=6,
∴梯形ABCD的面积=S△AOD+S△AOB+S△COB+S△COD=6+9+6+4=25.
故答案为25.
点评:本题考查了相似三角形的判定与性质及三角形的面积,用到的知识点:相似三角形的面积比等于相似比的平方;等高不等底的两个三角形的面积比等于其对应底边的比.
分析:设AC与BD交于点O.先由AB∥CD,得出△COD∽△AOB,根据相似三角形的面积比等于相似比的平方得到
 =(
=( )2=
)2= ,则
,则 =
= ,再根据等高不等底的两个三角形的面积比等于其对应底边的比得出
,再根据等高不等底的两个三角形的面积比等于其对应底边的比得出 =
= ,
, =
= ,求出S△AOD=S△COB=6,然后根据梯形ABCD的面积=S△AOD+S△AOB+S△COB+S△COD即可求解.
,求出S△AOD=S△COB=6,然后根据梯形ABCD的面积=S△AOD+S△AOB+S△COB+S△COD即可求解.解答:
 解:设AC与BD交于点O.
解:设AC与BD交于点O.∵AB∥CD,
∴△COD∽△AOB,
∴
 =(
=( )2=
)2= ,
,∴
 =
= .
.∵
 =
= ,
, =
= ,
,∴S△AOD=
 S△AOB=
S△AOB= ×9=6,S△COB=
×9=6,S△COB= S△COD=
S△COD= ×4=6,
×4=6,∴梯形ABCD的面积=S△AOD+S△AOB+S△COB+S△COD=6+9+6+4=25.
故答案为25.
点评:本题考查了相似三角形的判定与性质及三角形的面积,用到的知识点:相似三角形的面积比等于相似比的平方;等高不等底的两个三角形的面积比等于其对应底边的比.

练习册系列答案
相关题目
 如图,等腰梯形ABCD中,AD∥BC,以A为圆心,AD为半径的圆与BC切于点M,与AB交于点E,若AD=2,BC=6,则
如图,等腰梯形ABCD中,AD∥BC,以A为圆心,AD为半径的圆与BC切于点M,与AB交于点E,若AD=2,BC=6,则
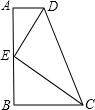 如图,直角梯形ABCD中,AB⊥BC,AD∥BC,点E是AB的中点,且AD+BC=DC、下列结论中:①△ADE∽△BEC;②DE2=DA•DC;③若设AD=a,CD=b,BC=c,则关于x的方程ax2+bx+c=0有两个不相等的实数根;④若设AD=a,AB=b,BC=c,则关于x的方程ax2+bx+c=0有两个相等的实数根.其中正确的结论有( )个.
如图,直角梯形ABCD中,AB⊥BC,AD∥BC,点E是AB的中点,且AD+BC=DC、下列结论中:①△ADE∽△BEC;②DE2=DA•DC;③若设AD=a,CD=b,BC=c,则关于x的方程ax2+bx+c=0有两个不相等的实数根;④若设AD=a,AB=b,BC=c,则关于x的方程ax2+bx+c=0有两个相等的实数根.其中正确的结论有( )个. 已知:如图,在梯形ABCD中,AD∥BC,AC⊥BD,AC=5,BD=12,若E是BC上的一点,BE=6.5,求DE的长.
已知:如图,在梯形ABCD中,AD∥BC,AC⊥BD,AC=5,BD=12,若E是BC上的一点,BE=6.5,求DE的长. 如图,若梯形ABCD的两条对角线与两底所围成的两个三角形的面积为4和9,则梯形的面积为
如图,若梯形ABCD的两条对角线与两底所围成的两个三角形的面积为4和9,则梯形的面积为