题目内容
在直角三角形ABC中,∠A=90°,AB=3cm,AC=4cm.(1)求BC的长;
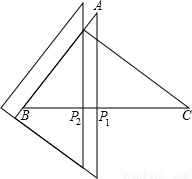
(2)点P为斜边BC上的一个动点(P与B、C不重合),PC=xcm,以点P为中心把△ABC按逆时针方向旋转90°至△DEF.
①当点P在如图所示的位置时,DF交AC、BC分别于点N、Q,EF交AC于点M,求MF的长;
②设△DEF与△ABC重叠部分的面积为ycm2,求出y与x的函数关系式及自变量x的取值范围.
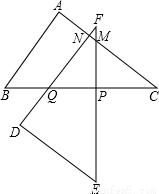
【答案】分析:(1)因为ABC为直角三角形,由两条边的长结合勾股定理求解即可.
(2)①由条件EF⊥BC于P,∠MPC=90°得出△PMC∽△ABC,根据比例关系求出MP的长,即可得出FM的长.
②先根据题意结合图形求出x的取值范围,得出当x=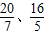 时为分界点,当x在不同区间时,面积有不同的求解方法,分不同的区间求解即可.
时为分界点,当x在不同区间时,面积有不同的求解方法,分不同的区间求解即可.
解答:解:(1)∵在直角三角形ABC中,∠A=90°,AB=3cm,AC=4cm,
∴根据勾股定理得BC=5cm.
(2)①∵绕点P旋转90°,EF⊥BC于P,∠MPC=90°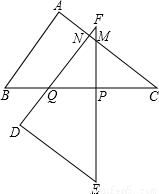
又∠C=∠C,
∴△PMC∽△ABC,
∴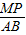 =
=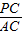 ,
,
∴MP=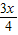 ,
,
∵PC=PM=x,
∴FM=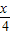 .
.
②当A与N重合时.
由PC=x可得MC=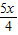 ,AM=4-
,AM=4-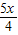
△FNM∽△CPM,
解得x=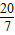 ;
;
当A与M重合时,容易求得x=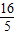 ,
,
i)当0<x≤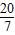 时
时
y=S△FPQ-S△FNM=S△CPM-S△FNM=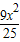 ;
;
ii)当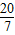 <x≤
<x≤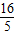 时
时
y=S△ABC-S△CPM=6-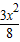 ;
;
iii)当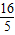 <x<5时,
<x<5时,
y=S△MPB=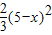 .
.
点评:本题考查了二次函数的运用,解题时要注意结合图形,分情况解题,不要漏掉一种情况.
(2)①由条件EF⊥BC于P,∠MPC=90°得出△PMC∽△ABC,根据比例关系求出MP的长,即可得出FM的长.
②先根据题意结合图形求出x的取值范围,得出当x=
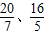 时为分界点,当x在不同区间时,面积有不同的求解方法,分不同的区间求解即可.
时为分界点,当x在不同区间时,面积有不同的求解方法,分不同的区间求解即可.解答:解:(1)∵在直角三角形ABC中,∠A=90°,AB=3cm,AC=4cm,
∴根据勾股定理得BC=5cm.
(2)①∵绕点P旋转90°,EF⊥BC于P,∠MPC=90°

又∠C=∠C,
∴△PMC∽△ABC,
∴
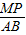 =
=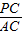 ,
,∴MP=
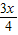 ,
,∵PC=PM=x,
∴FM=
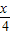 .
.②当A与N重合时.
由PC=x可得MC=
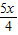 ,AM=4-
,AM=4-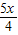
△FNM∽△CPM,
解得x=
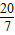 ;
;
当A与M重合时,容易求得x=
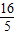 ,
,i)当0<x≤
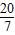 时
时y=S△FPQ-S△FNM=S△CPM-S△FNM=
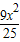 ;
;ii)当
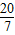 <x≤
<x≤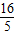 时
时y=S△ABC-S△CPM=6-
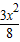 ;
;iii)当
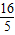 <x<5时,
<x<5时,y=S△MPB=
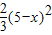 .
.点评:本题考查了二次函数的运用,解题时要注意结合图形,分情况解题,不要漏掉一种情况.

练习册系列答案
 期末集结号系列答案
期末集结号系列答案
相关题目
 6、如图,在直角三角形ABC中,∠ACB=90°,CA=4,点P是半圆弧AC的中点,连接BP,线段即把图形APCB(指半圆和三角形ABC组成的图形)分成两部分,则这两部分面积之差的绝对值是
6、如图,在直角三角形ABC中,∠ACB=90°,CA=4,点P是半圆弧AC的中点,连接BP,线段即把图形APCB(指半圆和三角形ABC组成的图形)分成两部分,则这两部分面积之差的绝对值是 使点B落在点E处,点C落在点D处.P、Q分别为线段AC、AD上的两个动点,且AQ=2PC,连接PQ交线段AE于点M.
使点B落在点E处,点C落在点D处.P、Q分别为线段AC、AD上的两个动点,且AQ=2PC,连接PQ交线段AE于点M. 如图,在直角三角形ABC中,∠C=90°,AC=20,BC=10,PQ=AB,P,Q两点分别在线段AC和过点A且垂直于AC的射线AM上运动,且点P不与点A,C重合,那么当点P运动到什么位置时,才能使△ABC与△APQ全等?
如图,在直角三角形ABC中,∠C=90°,AC=20,BC=10,PQ=AB,P,Q两点分别在线段AC和过点A且垂直于AC的射线AM上运动,且点P不与点A,C重合,那么当点P运动到什么位置时,才能使△ABC与△APQ全等?