题目内容
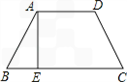
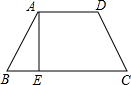 如图,这是一张等腰梯形纸片,它的上底AD长为2cm,下底BC长为4cm,腰长CD为2cm.求该梯形的高AE的长.
如图,这是一张等腰梯形纸片,它的上底AD长为2cm,下底BC长为4cm,腰长CD为2cm.求该梯形的高AE的长.分析:先作DF⊥BC于F,由四边形ABCD是等腰梯形,可知AB=CD,∠B=∠C,AE=DF,故△ABE≌△DCF,所以BE=CF=
(BC-AD)=2,在Rt△ABE中,根据勾股定理即可求出AE的长.
| 1 |
| 2 |
解答: 解:作DF⊥BC于F
解:作DF⊥BC于F
∵四边形ABCD是等腰梯形,
∴AB=CD,∠B=∠C,AE=DF,
∴△ABE≌△DCF,
∴BE=CF=
(BC-AD)=2
在Rt△ABE中,根据勾股定理
AE=
=
=
cm
答:该梯形的高AE的长为
cm.
 解:作DF⊥BC于F
解:作DF⊥BC于F ∵四边形ABCD是等腰梯形,
∴AB=CD,∠B=∠C,AE=DF,
∴△ABE≌△DCF,
∴BE=CF=
| 1 |
| 2 |
在Rt△ABE中,根据勾股定理
AE=
| AB2-BE2 |
| 22-12 |
| 3 |
答:该梯形的高AE的长为
| 3 |
点评:本题考查的是等腰梯形的性质及全等三角形的判定与性质,根据题意作出辅助线,构造出全等三角形是解答此题的关键.

练习册系列答案
 名师金手指领衔课时系列答案
名师金手指领衔课时系列答案
相关题目
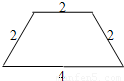
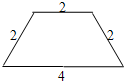 33、如图,这是一张等腰梯形纸片,它的上底长为2,下底长为4,腰长为2,这样的纸片共有5张.打算用其中的几张来拼成较大的等腰梯形,那么你能拼出哪几种不同的等腰梯形?分别画出它们的示意图,并写出它们的周长.
33、如图,这是一张等腰梯形纸片,它的上底长为2,下底长为4,腰长为2,这样的纸片共有5张.打算用其中的几张来拼成较大的等腰梯形,那么你能拼出哪几种不同的等腰梯形?分别画出它们的示意图,并写出它们的周长.