题目内容
15.计算:$\frac{1}{\sqrt{1}+\sqrt{2}}$+$\frac{1}{\sqrt{2}+\sqrt{3}}$+$\frac{1}{\sqrt{3}+\sqrt{4}}$+…+$\frac{1}{\sqrt{2000}+\sqrt{1999}}$.分析 先变形得到原式=$\frac{1}{\sqrt{2}+\sqrt{1}}$+$\frac{1}{\sqrt{3}+\sqrt{2}}$+$\frac{1}{\sqrt{4}+\sqrt{3}}$+…+$\frac{1}{\sqrt{2000}+\sqrt{1999}}$,然后进行分母有理化后合并即可.
解答 解:原式=$\frac{1}{\sqrt{2}+\sqrt{1}}$+$\frac{1}{\sqrt{3}+\sqrt{2}}$+$\frac{1}{\sqrt{4}+\sqrt{3}}$+…+$\frac{1}{\sqrt{2000}+\sqrt{1999}}$
=$\sqrt{2}$-1+$\sqrt{3}$-$\sqrt{2}$+$\sqrt{4}$-$\sqrt{3}$+…+$\sqrt{2000}$-$\sqrt{1999}$
=$\sqrt{2000}$-1
=20$\sqrt{5}$-1.
点评 本题考查了二次根式的计算:先把各二次根式化为最简二次根式,再进行二次根式的乘除运算,然后合并同类二次根式.

练习册系列答案
 中考利剑中考试卷汇编系列答案
中考利剑中考试卷汇编系列答案 教育世家状元卷系列答案
教育世家状元卷系列答案 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案 单元加期末复习先锋大考卷系列答案
单元加期末复习先锋大考卷系列答案
相关题目
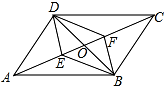 如图,在平行四边形ABCD中,对角线AC、BD相交于点O,E、F是对角线AC上的两点,给出下列四个条件:①AE=CF;②DE=BF;③∠ADE=∠CBF;④∠ABE=∠CDF.其中不能判定四边形DEBF是平行四边形的有( )
如图,在平行四边形ABCD中,对角线AC、BD相交于点O,E、F是对角线AC上的两点,给出下列四个条件:①AE=CF;②DE=BF;③∠ADE=∠CBF;④∠ABE=∠CDF.其中不能判定四边形DEBF是平行四边形的有( )