题目内容
化简求值,请选择一个你喜欢的x或者a、b值,代入求值.
(1)(1+
)÷
(2)
a+(1-a)+
(3)(
+
)÷
(4)(a-
)÷
;
(5)
÷
-1.
(1)(1+
| 1 |
| x-1 |
| x |
| x2-1 |
(2)
| 1 |
| 2 |
| a2-1 |
| a-1 |
(3)(
| x-1 |
| x+1 |
| 1 |
| x2-1 |
| 1 |
| x2-1 |
(4)(a-
| 2a-1 |
| a |
| 1-a2 |
| a2+a |
(5)
| a-b |
| a+2b |
| a2-b2 |
| a2+4ab+4b2 |
分析:(1)先计算括号内的部分,再将分子、分母中的部分因式分解,把除法转化为乘法,解答即可;
(2)先将
约分,再进行加减运算;
(3)将括号内和括号外部分因式分解,再将除法转化为乘法即可解答;
(4)先计算括号内的部分--通分,再将除法转化为乘法即可解答;
(5)先因式分解分子、分母中的部分,再将除法转化为乘法解答即可.
(2)先将
| a2-1 |
| a-1 |
(3)将括号内和括号外部分因式分解,再将除法转化为乘法即可解答;
(4)先计算括号内的部分--通分,再将除法转化为乘法即可解答;
(5)先因式分解分子、分母中的部分,再将除法转化为乘法解答即可.
解答:解:(1)原式=(
+
)•
=
•
=x+1;
当x=2时,原式=2+1=3;
(2)原式=
a+1-a+
=
a+1-a+a+1
=
a+2;
当a=2时,原式=
×2+2=3;
(3)原式=(
+
)•(x2-1)
=(
+
)•(x-1)(x+1)
=
•(x-1)(x+1)+
(x-1)(x+1)
=(x-1)2+1
=x2-2x+1+1
=x2-2x+2;
当x=2时,原式=22-2×2+2
=4-4+2
=2;
(4)原式=
•
=
•
=1-a;
当x=2时,原式=1-2=-1;
(5)原式=
•
-1
=
-1
=
=
;
当a=1,b=2时,原式=
=
.
| x-1 |
| x-1 |
| 1 |
| x-1 |
| (x-1)(x+1) |
| x |
=
| x |
| x-1 |
| (x-1)(x+1) |
| x |
=x+1;
当x=2时,原式=2+1=3;
(2)原式=
| 1 |
| 2 |
| (a-1)(a+1) |
| (a-1) |
=
| 1 |
| 2 |
=
| 1 |
| 2 |
当a=2时,原式=
| 1 |
| 2 |
(3)原式=(
| x-1 |
| x+1 |
| 1 |
| x2-1 |
=(
| x-1 |
| x+1 |
| 1 |
| x2-1 |
=
| x-1 |
| x+1 |
| 1 |
| (x-1)(x+1) |
=(x-1)2+1
=x2-2x+1+1
=x2-2x+2;
当x=2时,原式=22-2×2+2
=4-4+2
=2;
(4)原式=
| a2-2a+1 |
| a |
| a(a+1) |
| (1-a)(1+a) |
=
| (a-1)2 |
| a |
| a(a+1) |
| (1-a)(1+a) |
=1-a;
当x=2时,原式=1-2=-1;
(5)原式=
| a-b |
| a+2b |
| (a+2b)2 |
| (a-b)(a+b) |
=
| a+2b |
| a+b |
=
| a+2b-a-b |
| a+b |
=
| b |
| a+b |
当a=1,b=2时,原式=
| 2 |
| 1+2 |
| 2 |
| 3 |
点评:本题考查了分式的化简求值,要熟悉因式分解及分式的运算法则,要注意,取喜爱的数代入求值时,要特注意原式及化简过程中的每一步都有意义.

练习册系列答案
相关题目
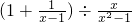


 ;
;  .
.