题目内容
 如图圆的半径为10,将圆的劣弧AB沿弦AB翻折后所得圆弧恰好经过圆心O,则折痕AB的长为( )
如图圆的半径为10,将圆的劣弧AB沿弦AB翻折后所得圆弧恰好经过圆心O,则折痕AB的长为( )分析:先过点O作OD⊥AB,垂足为D,连接OA,由题意求得OD,由勾股定理求得AD,再由垂径定理求得AB的值即可.
解答: 解:作OD⊥AB于D,连接OA.
解:作OD⊥AB于D,连接OA.
∵OD⊥AB,
∴AB=2AD,
∵OD=
OA=
×10=5,
∴AD=
=
=5
,
∴AB=2AD=2×5
=10
.
 解:作OD⊥AB于D,连接OA.
解:作OD⊥AB于D,连接OA.∵OD⊥AB,
∴AB=2AD,
∵OD=
| 1 |
| 2 |
| 1 |
| 2 |
∴AD=
| OA2-OD2 |
| 102-52 |
| 3 |
∴AB=2AD=2×5
| 3 |
| 3 |
点评:本题考查了勾股定理和垂径定理的知识.此题比较简单,解此题的关键是掌握折叠的性质,注意数形结合思想的应用.

练习册系列答案
 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案
相关题目
 如图是一位同学从照片上剪切下来的画面,“图上”太阳与海平线交于A、B两点,他测得“图上”圆的半径为10厘米,AB=16厘米,若从目前太阳所处位置到太阳完全跳出海面的时间为10分钟,则“图上”太阳升起的速度为( )
如图是一位同学从照片上剪切下来的画面,“图上”太阳与海平线交于A、B两点,他测得“图上”圆的半径为10厘米,AB=16厘米,若从目前太阳所处位置到太阳完全跳出海面的时间为10分钟,则“图上”太阳升起的速度为( )| A、0.4厘米/分 | B、0.6厘米/分 | C、1.0厘米/分 | D、1.6厘米/分 |
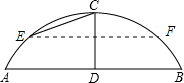 (2012•松江区二模)某公园有一圆弧形的拱桥,如图已知拱桥所在圆的半径为10米,拱桥顶D到水面AB的距离DC=4米.
(2012•松江区二模)某公园有一圆弧形的拱桥,如图已知拱桥所在圆的半径为10米,拱桥顶D到水面AB的距离DC=4米. 如图所示,一座圆弧形的拱桥,它所在圆的半径为10米,某天通过拱桥的水面宽度AB为16米,现有一小帆船高出水面的高度是3.5米,问小船能否从拱桥下通过?
如图所示,一座圆弧形的拱桥,它所在圆的半径为10米,某天通过拱桥的水面宽度AB为16米,现有一小帆船高出水面的高度是3.5米,问小船能否从拱桥下通过? 如图圆的半径为10,将圆的劣弧AB沿弦AB翻折后所得圆弧恰好经过圆心O,则折痕AB的长为
如图圆的半径为10,将圆的劣弧AB沿弦AB翻折后所得圆弧恰好经过圆心O,则折痕AB的长为

