题目内容
11.已知直线y=-$\frac{\sqrt{3}}{3}$x+1与x轴、y轴分别交于A、B两点,以AB为边在第一象限内作正三角形ABC,点D为AB的中点,将△ACB折叠,使点C与D重合,试求折痕EF所在直线的解析式.(提示:直角三角形中,如果一条直角边等于斜边的一半,那么这条直角边所对的角为30°)分析 首先求出图象与坐标轴的交点,进而得出等边三角形的边长,再利用两直线平行时其一次项系数相等,结合已知得出F点坐标,进而求出函数解析式.
解答 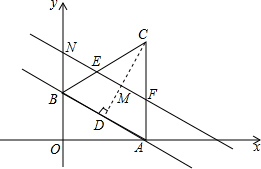 解:∵直线y=-$\frac{\sqrt{3}}{3}$x+1与x轴、y轴分别交于A、B两点,
解:∵直线y=-$\frac{\sqrt{3}}{3}$x+1与x轴、y轴分别交于A、B两点,
∴当x=0时,y=1,则B(0,1),
当y=0时,x=$\sqrt{3}$,则A($\sqrt{3}$,0),
如图所示:由题意可得,CM=DM,EF∥AB,
∵正三角形ABC,点D为AB的中点,
∴CD⊥AB,CD⊥EF,
∵OB=1,AO=$\sqrt{3}$,
∴AB=AC=BC=2,
∴AF=1,
∴F($\sqrt{3}$,1),
设直线EF的解析式为:y=-$\frac{\sqrt{3}}{3}$x+b,
故1=-$\frac{\sqrt{3}}{3}$×$\sqrt{3}$+b,
解得:b=2,
故直线EF的解析式为:y=-$\frac{\sqrt{3}}{3}$x+2.
点评 本题考查的是一次函数综合题,涉及到等边三角形的性质、用待定系数法求一次函数的解析式等知识,得出EF∥AB得出直线解析式一次项系数相等是解题关键.

练习册系列答案
 夺冠训练单元期末冲刺100分系列答案
夺冠训练单元期末冲刺100分系列答案 新思维小冠军100分作业本系列答案
新思维小冠军100分作业本系列答案 名师指导一卷通系列答案
名师指导一卷通系列答案
相关题目
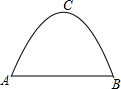 如图所示,某工厂大门是一抛物线形水泥建筑物,大门地面宽AB=4m,顶部C离地面高度为4m,现有一辆满载货物的汽车欲通过大门,货物顶部距离地面2m,装货宽度为2.5m,试判断这辆汽车能否顺利通过大门?通过计算说明.
如图所示,某工厂大门是一抛物线形水泥建筑物,大门地面宽AB=4m,顶部C离地面高度为4m,现有一辆满载货物的汽车欲通过大门,货物顶部距离地面2m,装货宽度为2.5m,试判断这辆汽车能否顺利通过大门?通过计算说明.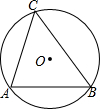 已知:如图,在△ABC中,AB=10,∠C=60°,求△ABC外接圆⊙O的半径r.
已知:如图,在△ABC中,AB=10,∠C=60°,求△ABC外接圆⊙O的半径r.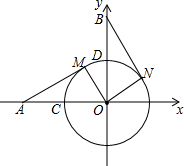 已知,如图坐标轴上点A(-4,0)、B(0,4),以点O为圆心,2为半径作⊙O与x轴的负半轴、y轴的正半轴分别交于点C、D,将扇形COD绕点O顺时针旋转α°得到扇形MON(点M与点C、点N与点D对应,其中0°≤α≤360°),连接AM、BN.
已知,如图坐标轴上点A(-4,0)、B(0,4),以点O为圆心,2为半径作⊙O与x轴的负半轴、y轴的正半轴分别交于点C、D,将扇形COD绕点O顺时针旋转α°得到扇形MON(点M与点C、点N与点D对应,其中0°≤α≤360°),连接AM、BN.