题目内容
 如图△ABC中,∠C=90°,AD平分∠BAC,DE⊥AB于E,下面等式错误的是( )
如图△ABC中,∠C=90°,AD平分∠BAC,DE⊥AB于E,下面等式错误的是( )| A、AC2+DC2=AD2 | ||
| B、AD2-DE2=AE2 | ||
| C、AD2=DE2+AC2 | ||
D、BD2-BE2=
|
分析:先证得△AED≌△ACD,从而根据全等的性质得出AE=AC、然后根据勾股定理两条直角边长的平方之和一定等于斜边长的平方结合各选项即可作出判断.
解答:解:∵AD平分∠BAC,DE⊥AB于E,
∴DE=DC,∠EAD=∠CAD,
在RT△AED和△ACD中,
,
∴△AED≌△ACD,即可得AE=AC.
A、在RT△ADC中可得出AC2+DC2=AD2,故本选项错误;
B、在RT△ADE中可得出AD2-DE2=AE2,故本选项错误;
C、在RT△ADE中可得出AD2=DE2+AE2,而AE=AC,故可得AD2=DE2+AC2,故本选项错误;
D、在RT△BDE中BD2-BE2=ED2=DC2,而DC≠BD≠
BC,可得BD2-BE2≠
BC2,故本选项正确.
故选D.
∴DE=DC,∠EAD=∠CAD,
在RT△AED和△ACD中,
|
∴△AED≌△ACD,即可得AE=AC.
A、在RT△ADC中可得出AC2+DC2=AD2,故本选项错误;
B、在RT△ADE中可得出AD2-DE2=AE2,故本选项错误;
C、在RT△ADE中可得出AD2=DE2+AE2,而AE=AC,故可得AD2=DE2+AC2,故本选项错误;
D、在RT△BDE中BD2-BE2=ED2=DC2,而DC≠BD≠
| 1 |
| 2 |
| 1 |
| 4 |
故选D.
点评:本题考查勾股定理及角平分线的性质,属于基础知识的考查,涉及了一些等线段的转换,同学们要注意根据角平分线的性质及全等三角形的性质得出某些线段的相等关系.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
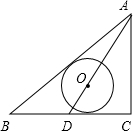 如图△ABC中,∠C=90°,AC=6,AB=10,D是BC边的中点,以AD上一点O为圆心的圆与AB,BC都相切,则⊙O的半径为( )
如图△ABC中,∠C=90°,AC=6,AB=10,D是BC边的中点,以AD上一点O为圆心的圆与AB,BC都相切,则⊙O的半径为( )A、
| ||
B、
| ||
C、
| ||
| D、2 |
 8、如图△ABC中,AB=3,AC=2,BO平分∠ABC,CO平分∠ACB.DE过点O交AB于D,交AC于E,且DE∥BC.则△ADE周长为
8、如图△ABC中,AB=3,AC=2,BO平分∠ABC,CO平分∠ACB.DE过点O交AB于D,交AC于E,且DE∥BC.则△ADE周长为 (2013•南岗区一模)如图△ABC中,DE∥BC,CD、BE交于点F,若DF=1,CF=3,AD=2,则线段BD的长等于
(2013•南岗区一模)如图△ABC中,DE∥BC,CD、BE交于点F,若DF=1,CF=3,AD=2,则线段BD的长等于 如图△ABC中,∠A=78°,AB=AC,P为△ABC内一点,连BP,CP,使∠PBC=9°,∠PCB=30°,连PA,则∠BAP的度数为
如图△ABC中,∠A=78°,AB=AC,P为△ABC内一点,连BP,CP,使∠PBC=9°,∠PCB=30°,连PA,则∠BAP的度数为 如图△ABC中,∠ABC=20°,外角∠ABF的平分线与CA边的延长线交于点D,外角∠EAC的平分线交BC边的延长线于点H,若∠BDA=∠DAB,则∠AHC=( )度.
如图△ABC中,∠ABC=20°,外角∠ABF的平分线与CA边的延长线交于点D,外角∠EAC的平分线交BC边的延长线于点H,若∠BDA=∠DAB,则∠AHC=( )度.