题目内容
【题目】在平面直角坐标系![]() 中,点
中,点![]() 在抛物线
在抛物线![]() 上.
上.
(1)如图1,若抛物线经过点![]() .
.
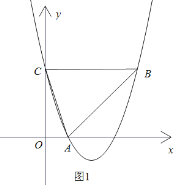
①求抛物线的解析式;
②设抛物线与![]() 轴交于点
轴交于点![]() ,连接
,连接![]() ,
,![]() ,
,![]() ,若点
,若点![]() 在抛物线上,且
在抛物线上,且![]() 与
与![]() 的面积相等,求点
的面积相等,求点![]() 的坐标;
的坐标;
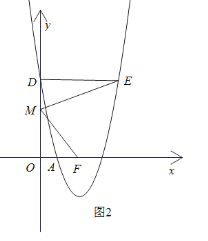
(2)如图2,若抛物线与![]() 轴交于点D过点
轴交于点D过点![]() 作
作![]() 轴的平行线交抛物线于另一点
轴的平行线交抛物线于另一点![]() .点
.点![]() 为抛物线的对称轴与
为抛物线的对称轴与![]() 轴的交点,
轴的交点,![]() 为线段
为线段![]() 上一动点.若以M,D,E为顶点的三角形与
上一动点.若以M,D,E为顶点的三角形与![]() 相似.并且符合条件的点
相似.并且符合条件的点![]() 恰有
恰有![]() 个,请直接写出抛物线的解析式及相应的点
个,请直接写出抛物线的解析式及相应的点![]() 的坐标.
的坐标.
【答案】(1)①![]() ;②
;②![]() ;(2)当抛物线的解析式为
;(2)当抛物线的解析式为![]() 时,点
时,点![]() 的坐标为
的坐标为![]() 或
或![]() ;当抛物线
;当抛物线![]() 的解析式为时,点
的解析式为时,点![]() 的坐标为
的坐标为![]() 或
或![]()
【解析】
(1)①利用待定系数法直接求抛物线的解析式;
②先求解![]() 的面积为
的面积为![]() 分情况讨论:当
分情况讨论:当![]() 在
在![]() 的下方时,过点
的下方时,过点![]() 作
作![]() 轴交
轴交![]() 于
于![]() ,设点
,设点![]() 利用
利用![]() 的面积为
的面积为![]() ,建立方程求解即可,当
,建立方程求解即可,当![]() 在
在![]() 的上方时,过点
的上方时,过点![]() 作
作![]() 的平行线,与抛物线的另一交点即为点
的平行线,与抛物线的另一交点即为点![]() ,利用函数的交点可得答案;
,利用函数的交点可得答案;
(2)先求解抛物线的解析式为:![]() ,得到
,得到![]() .
.
设![]() ,利用相似三角形的性质建立方程,由方程解的情况讨论得出结论.
,利用相似三角形的性质建立方程,由方程解的情况讨论得出结论.
解:![]() ①
①![]() 抛物线过点
抛物线过点![]() 和点
和点![]()
![]()
解得![]()
![]() 抛物线的解析式为
抛物线的解析式为![]()
②在![]() 中,令
中,令![]() 得
得![]() ,
,
![]() 点
点![]() 的坐标为
的坐标为![]()
![]()
点![]() 到
到![]() 的距离为
的距离为![]()
![]()
设直线![]() 的解析式为
的解析式为![]()
则![]()
解得![]()
![]() 直线
直线![]() 的解析式为
的解析式为![]()
(I)如图,若点![]() 在直线
在直线![]() 下方的抛物线上,过点
下方的抛物线上,过点![]() 作
作![]() 轴交
轴交![]() 于
于![]()
设点![]()
则点![]()
![]()
![]() 无解
无解
此时点![]() 不存在
不存在
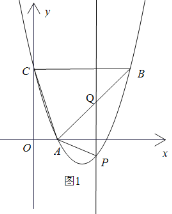
(II)若点![]() 在直线
在直线![]() 上方的抛物线上,过点
上方的抛物线上,过点![]() 作
作![]() 的平行线,与抛物线的另一交点即为点
的平行线,与抛物线的另一交点即为点![]() ,则
,则![]()
则可设直线![]() 的解析式为
的解析式为![]()
将![]() 代入,得
代入,得![]()
![]() 直线
直线![]() 的解析式为
的解析式为![]()
令![]()
解得![]() 或
或![]() (舍去
(舍去![]() )
)
![]()

![]() 当抛物线的解析式为
当抛物线的解析式为![]() 时,点
时,点![]() 的坐标为
的坐标为![]() 或
或![]()
当抛物线的解析式为![]() 时,点
时,点![]() 的坐标为
的坐标为![]() 或
或![]()
理由如下:由点![]() 在拋物线
在拋物线![]() 上,得
上,得![]()
![]() 抛物线的解析式为
抛物线的解析式为![]()
![]()
设![]()
当![]() 时,
时,![]()
即![]()
![]()
当![]() 时,
时,![]()
即![]()
![]()
![]() 当方程
当方程![]() 有两个相等实数根时,
有两个相等实数根时,
![]()
解得![]() (负值舍去)
(负值舍去)
此时,方程![]() 有两个相等实数根
有两个相等实数根![]()
方程![]() 有一个实数根
有一个实数根![]() ,符合题意
,符合题意
此时抛物线的解析式为![]()
点![]() 的坐标为
的坐标为![]() 或
或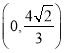
![]() 当方程
当方程![]() 有两个不相等的实数根时,
有两个不相等的实数根时,
把![]() 代入
代入![]() ,解得
,解得![]() 负值舍去)
负值舍去)
此时,方程![]() 有两个不相等的实数根
有两个不相等的实数根![]()
方程![]() 有一个实数根
有一个实数根![]() ,符合题意;
,符合题意;
此时抛物线的解析式为![]()
点![]() 的坐标为
的坐标为![]() 或
或![]()
综上所述,当抛物线的解析式为![]()
点![]() 的坐标为
的坐标为![]() 或
或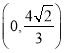 ;
;
当抛物线的解析式为![]() 时,
时,
点![]() 的坐标为
的坐标为![]() 或
或![]()

 名校课堂系列答案
名校课堂系列答案