题目内容
如图,在平面直角坐标系中,点O为坐标原点,直线AB分别交x、y轴于A、B两点,点A的坐标为(3,0),点B的坐标为(0,6),点C是x轴负半轴上一点,过O点作BC的垂线,垂足为D,过B点作AD的垂线交OD、AD于点F和点K,交AC于点E,OF:CD=2:3.
(1)求直线AB的解析式;
(2)动点P从B点出发沿BC方向向终点C匀速运动(不包括B、C两点),速度为每秒2 个单位长度,过P作x轴的平行线交AB于点N,设点P的运动时间为t,线段AN长为d,求d与t之间的函数关系式,并直接写出自变量t的取值范围;
个单位长度,过P作x轴的平行线交AB于点N,设点P的运动时间为t,线段AN长为d,求d与t之间的函数关系式,并直接写出自变量t的取值范围;
(3)在(2)的条件下,动点Q从A点出发沿AC方向向终点C匀速运动,速度为每秒 个单位长度,设P、Q两点同时出发,当一点到达终点时另一点停止运动,连接ON,当AD平分线段NQ时,求此时t的值.
个单位长度,设P、Q两点同时出发,当一点到达终点时另一点停止运动,连接ON,当AD平分线段NQ时,求此时t的值.
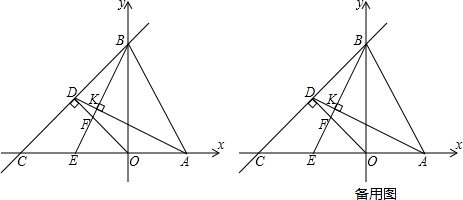
解:(1)设直线AB的解析式为y=kx+b,
把A(3,0)、B(0,6)代入y=kx+b,得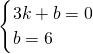 ,
,
解得: ,
,
则直线AB的解析式为y=-2x+6;
(2)设AD与y轴交于点S,
∵OD⊥BC,
∴∠DCA+∠DOC=90°,
又∵∠FOB+∠DOC=90°,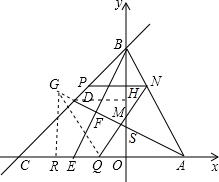
∴∠DCA=∠FOB,
∵BE⊥AD,
∴∠BFA=90°,
∵x轴⊥y轴,
∴∠SOA=90°,
∴∠BFA=∠SOA,
又∵∠FSB=∠OSA,
∴∠FBO=∠DAC,
∴△DCA∽△FOB,
∴BC2=CE•CD,
∵BO=6,AO=3,
∴AC=9,
∴C(-6,0),
∴BC=6 ,AB=3
,AB=3 ,
,
当P在线段BC上运动时,
∵PN∥x轴,
∴ =
=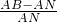 ,即
,即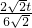 =
=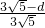 ,
,
∴d=- t+3
t+3 (0<t<3);
(0<t<3);
(3)设NQ与AD交于点M,延长AD到G,使得MG=AM,连接QG,
∵MN=MQ,∠AMN=∠QMG,
∴△ANM≌△GQM(SAS),
∴∠ANM=∠GQM,GQ=AN=d=- t+3
t+3 ,
,
∴AN∥GQ,
∴∠CQG=∠OAB,
∴tan∠OAB=tan∠GQC=2,过G点作GR⊥AC,垂足为R,
∴设RQ=a,则GR=2a,
∴GQ=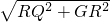 =
= a,
a,
过D作DH⊥BO于点H,
∵OB=OC,∠ACB=45°,OD⊥BC,
∴CD=BD,DH=BH=HO= CO=3,
CO=3,
∴DH=AO,
在△DSH和△ASO中,∠HDA=∠DAO,DH=AO,∠DSH=∠AOS,
∴△DSH≌△ASO(ASA),
∴HS=SO= HO=
HO= ,tan∠DAC=
,tan∠DAC=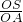 =
=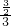 =
= ,
,
∴AR=4a,
∴AQ=AR-RQ=4a-3a=3a,
又∵AQ= t,GQ=AN=d=-
t,GQ=AN=d=- t+3
t+3 ,
,
∴ ,
,
解得:t= .
.
分析:(1)设直线AB解析式为y=kx+b,将A与B坐标代入求出k与b的值,即可确定出AB解析式;
(2)设AD与y轴交于S点,利用相似三角形的判定与性质,求得一次函数解析式;
(3)设NQ与AD交于点M,延长AD到G,使得MG=AM,连接QG,利用三角形全等的判定与性质,相似三角形的判定与性质,以及一次函数解决问题.
点评:此题综合考查了待定系数法求一次函数解析式,三角形全等的判定与性质,相似三角形的判定与性质以及有关锐角三角函数的意义等问题.
把A(3,0)、B(0,6)代入y=kx+b,得
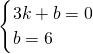 ,
,解得:
 ,
,则直线AB的解析式为y=-2x+6;
(2)设AD与y轴交于点S,
∵OD⊥BC,
∴∠DCA+∠DOC=90°,
又∵∠FOB+∠DOC=90°,

∴∠DCA=∠FOB,
∵BE⊥AD,
∴∠BFA=90°,
∵x轴⊥y轴,
∴∠SOA=90°,
∴∠BFA=∠SOA,
又∵∠FSB=∠OSA,
∴∠FBO=∠DAC,
∴△DCA∽△FOB,
∴BC2=CE•CD,
∵BO=6,AO=3,
∴AC=9,
∴C(-6,0),
∴BC=6
 ,AB=3
,AB=3 ,
,当P在线段BC上运动时,
∵PN∥x轴,
∴
 =
=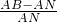 ,即
,即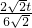 =
=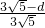 ,
,∴d=-
 t+3
t+3 (0<t<3);
(0<t<3);(3)设NQ与AD交于点M,延长AD到G,使得MG=AM,连接QG,
∵MN=MQ,∠AMN=∠QMG,
∴△ANM≌△GQM(SAS),
∴∠ANM=∠GQM,GQ=AN=d=-
 t+3
t+3 ,
,∴AN∥GQ,
∴∠CQG=∠OAB,
∴tan∠OAB=tan∠GQC=2,过G点作GR⊥AC,垂足为R,
∴设RQ=a,则GR=2a,
∴GQ=
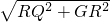 =
= a,
a,过D作DH⊥BO于点H,
∵OB=OC,∠ACB=45°,OD⊥BC,
∴CD=BD,DH=BH=HO=
 CO=3,
CO=3,∴DH=AO,
在△DSH和△ASO中,∠HDA=∠DAO,DH=AO,∠DSH=∠AOS,
∴△DSH≌△ASO(ASA),
∴HS=SO=
 HO=
HO= ,tan∠DAC=
,tan∠DAC=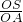 =
=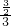 =
= ,
,∴AR=4a,
∴AQ=AR-RQ=4a-3a=3a,
又∵AQ=
 t,GQ=AN=d=-
t,GQ=AN=d=- t+3
t+3 ,
,∴
 ,
,解得:t=
 .
.分析:(1)设直线AB解析式为y=kx+b,将A与B坐标代入求出k与b的值,即可确定出AB解析式;
(2)设AD与y轴交于S点,利用相似三角形的判定与性质,求得一次函数解析式;
(3)设NQ与AD交于点M,延长AD到G,使得MG=AM,连接QG,利用三角形全等的判定与性质,相似三角形的判定与性质,以及一次函数解决问题.
点评:此题综合考查了待定系数法求一次函数解析式,三角形全等的判定与性质,相似三角形的判定与性质以及有关锐角三角函数的意义等问题.

练习册系列答案
 课课练江苏系列答案
课课练江苏系列答案 名牌中学课时作业系列答案
名牌中学课时作业系列答案 明天教育课时特训系列答案
明天教育课时特训系列答案 浙江新课程三维目标测评课时特训系列答案
浙江新课程三维目标测评课时特训系列答案
相关题目
 如图,在平面直角坐标中,四边形OABC是等腰梯形,CB∥OA,OA=7,AB=4,∠COA=60°,点P为x轴上的一个动点,但是点P不与点0、点A重合.连接CP,D点是线段AB上一点,连接PD.
如图,在平面直角坐标中,四边形OABC是等腰梯形,CB∥OA,OA=7,AB=4,∠COA=60°,点P为x轴上的一个动点,但是点P不与点0、点A重合.连接CP,D点是线段AB上一点,连接PD. (2012•渝北区一模)如图,在平面直角坐标xoy中,以坐标原点O为圆心,3为半径画圆,从此圆内(包括边界)的所有整数点(横、纵坐标均为整数)中任意选取一个点,其横、纵坐标之和为0的概率是
(2012•渝北区一模)如图,在平面直角坐标xoy中,以坐标原点O为圆心,3为半径画圆,从此圆内(包括边界)的所有整数点(横、纵坐标均为整数)中任意选取一个点,其横、纵坐标之和为0的概率是 如图,在平面直角坐标中,等腰梯形ABCD的下底在x轴上,且B点坐标为(4,0),D点坐标为(0,3),则AC长为
如图,在平面直角坐标中,等腰梯形ABCD的下底在x轴上,且B点坐标为(4,0),D点坐标为(0,3),则AC长为 如图,在平面直角坐标xOy中,已知点A(-5,0),P是反比例函数
如图,在平面直角坐标xOy中,已知点A(-5,0),P是反比例函数 ∠COA=45°,动点P从点O出发,在梯形OABC的边上运动,路径为O→A→B→C,到达点C时停止.作直线CP.
∠COA=45°,动点P从点O出发,在梯形OABC的边上运动,路径为O→A→B→C,到达点C时停止.作直线CP.