题目内容
点C、D在直线AB上,线段AC、CB、AD、DB的长满足AC:CB=5:4,AD:DB=2:1,且CD=2cm,则线段AB的长为分析:根据A,B,C,D不同位置关系,得出它们的不同长度,进而分别求出AB的长度,注意利用图形分析即可得出.
解答:解:设AB长为xcm,第一种情况:
点C,D在直线AB上,线段AC,CB,AD,DB的长度满足AC:CB=5:4,
那么AC=
AB,
又因为AD:DB=2:1,那么AD=
AB,
AD-AD=
AB-
AB,
既CD=
AB,因为CD=2cm,所以AB=18cm;

第二种情况:

AD=
AB (同第一种情况) AC=
AB=5AB,
CD=AC-AD=(5-
)AB=
AB=2,
∴AB=
cm;
第三种情况:
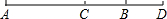
AC=
AB (同第一种情况) AD=
AB=2AB,
CD=AD-AC=(2-
)AB=
AB=2,
∴AB=
cm;
第四种情况:
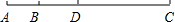
AC=5AB (同第二种情况),
AD=2AB(同第三种情况).
CD=AC-AD=3AB=2,
AB=
cm,
故答案为:18cm或
cm或
或
cm.
点C,D在直线AB上,线段AC,CB,AD,DB的长度满足AC:CB=5:4,
那么AC=
| 5 |
| 9 |
又因为AD:DB=2:1,那么AD=
| 2 |
| 3 |
AD-AD=
| 2 |
| 3 |
| 5 |
| 9 |
既CD=
| 1 |
| 9 |

第二种情况:

AD=
| 2 |
| 3 |
| 5 |
| 5-4 |
CD=AC-AD=(5-
| 2 |
| 3 |
| 13 |
| 3 |
∴AB=
| 6 |
| 13 |
第三种情况:
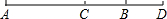
AC=
| 5 |
| 9 |
| 2 |
| 2-1 |
CD=AD-AC=(2-
| 5 |
| 9 |
| 13 |
| 9 |
∴AB=
| 18 |
| 13 |
第四种情况:
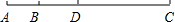
AC=5AB (同第二种情况),
AD=2AB(同第三种情况).
CD=AC-AD=3AB=2,
AB=
| 2 |
| 3 |
故答案为:18cm或
| 8 |
| 13 |
| 6 |
| 13 |
| 2 |
| 3 |
点评:此题主要考查了两点之间的距离求法,根据已知A,B,C,D不同位置得出不同图形是解题关键,此题容易出错漏解.

练习册系列答案
相关题目
 飞行最大高度OM=5米,圆柱形桶的直径为0.5米,高为0.3米(网球的体积和圆柱形桶的厚度忽略不计).
飞行最大高度OM=5米,圆柱形桶的直径为0.5米,高为0.3米(网球的体积和圆柱形桶的厚度忽略不计).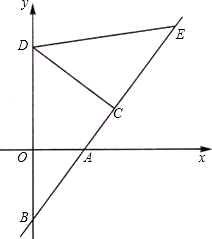 的垂线交y轴于点D,且OD=CD=CE.点C的坐标为(a,b),a、b(a>b)是方程x2-12x+32=0的解.
的垂线交y轴于点D,且OD=CD=CE.点C的坐标为(a,b),a、b(a>b)是方程x2-12x+32=0的解. 如图,已知:点M、N在直线AB上,∠AMC=∠BND,∠CME=∠DNF=90°,则除去已知角外,图中小于平角且相等的角还有
如图,已知:点M、N在直线AB上,∠AMC=∠BND,∠CME=∠DNF=90°,则除去已知角外,图中小于平角且相等的角还有