题目内容
28、仅通过观察、试验等可以寻找规律，但是由于观察可能有误差，这样仅通过观察、试验等就下结论有时也缺乏说服力，所以得出的结论还需要证明．已知△ABC，求证：∠A+∠B+∠C=180°．
分析：由题意，过C作CD∥AB，则∠A=∠ACD，再根据平行线的性质，证明即可．
解答：
证明：如图，过C作CD∥AB，
∴∠A=∠ACD，
∴∠A+∠ACB=∠BCD，
∵CD∥AB，
∴∠B+∠BCD=180°，
∴∠B+∠A+∠ACB=180°，即∠A+∠B+∠C=180°．
证明：如图，过C作CD∥AB，∴∠A=∠ACD，
∴∠A+∠ACB=∠BCD，
∵CD∥AB，
∴∠B+∠BCD=180°，
∴∠B+∠A+∠ACB=180°，即∠A+∠B+∠C=180°．
点评：本题主要考查了三角形的内角和定理，解答此题的关键是过C点作出AB的平行线，利用平行线的性质解答．
练习册系列答案
相关题目
=k（其中k＞0），请写出 线段BG、DE的数量关系及位置关系．请选择图5或图6证明你的判断（仅证数量关系）．
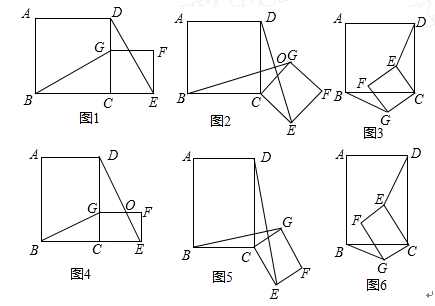
仅通过观察、试验等可以寻找规律，但是由于观察可能有误差，这样仅通过观察、试验等就下结论有时也缺乏说服力，所以得出的结论还需要证明．
