题目内容
【题目】己知抛物线![]()
![]() 与
与![]() 轴最多有一个交点,现有以下三个结论:①该抛物线的对称轴在
轴最多有一个交点,现有以下三个结论:①该抛物线的对称轴在![]() 轴右侧;②关于
轴右侧;②关于![]() 的方程
的方程![]() 无实数根;③
无实数根;③![]() ;其中,正确结论的个数为( )
;其中,正确结论的个数为( )
A.0个B.1个C.2个D.3个
【答案】C
【解析】
①根据a、b同号可确定对称轴位置;
②根据抛物线![]() (b>a>0)与x轴有一个交点,知y≥0,所以y≠-1;
(b>a>0)与x轴有一个交点,知y≥0,所以y≠-1;
③因为对称轴![]() <0,所以x=2时,y>0.
<0,所以x=2时,y>0.
解:①∵b>a>0,即a、b同号,
∴该抛物线的对称轴在y轴左侧; 故①不正确;
②如果抛物线![]() (b>a>0)与x轴有一个交点,
(b>a>0)与x轴有一个交点,
则这个交点就是抛物线的顶点,
如果抛物线![]() (b>a>0)与x轴没有交点,
(b>a>0)与x轴没有交点,
则y>0, ∴y≠-1,
即关于x的方程![]() 无实数根; 故②正确;
无实数根; 故②正确;
③由①知:抛物线的对称轴在y轴左侧;
∴对称轴![]() <0,
<0,
∵抛物线![]() (b>a>0)与x轴最多有一个交点,
(b>a>0)与x轴最多有一个交点,
∴y≥0, ∴4a+2b+c>0; 故③正确;
故选:C.

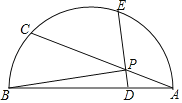
【题目】如图,以![]() 为直径的半圆上有一点
为直径的半圆上有一点![]() ,连接
,连接![]() ,点
,点![]() 是
是![]() 上一个动点,连接
上一个动点,连接![]() ,作
,作![]() 交
交![]() 于点
于点![]() ,交半圆于点
,交半圆于点![]() .已知:
.已知:![]() ,设
,设![]() 的长度为
的长度为![]() ,
,![]() 的长度为
的长度为![]() ,
,![]() 的长度为
的长度为![]() (当点
(当点![]() 与点
与点![]() 重合时,
重合时,![]() ,
,![]() ,当点
,当点![]() 与点
与点![]() 重合时,
重合时,![]() ,
,![]() ).
).
小青同学根据学习函数的经验,分别对函数![]() ,
,![]() 随自变量
随自变量![]() 变化而变化的规律进行了探究.
变化而变化的规律进行了探究.
下面是小青同学的探究过程,请补充完整:
(1)按照下表中自变量![]() 的值进行取点、画图、测量,分别得到了
的值进行取点、画图、测量,分别得到了![]() ,
,![]() 与
与![]() 的几组对应值,请补全表格;
的几组对应值,请补全表格;
| 0 | 0.5 | 1 | 1.5 | 2 | 2.5 | 3 | 3.5 | 4 | 4.5 | 5 |
| 5 | 2.85 | 1.98 | 1.52 | 1.21 | 0.97 | 0.76 | 0.56 | 0.37 | 0.19 | 0 |
| 0 | 0.46 | 1.29 | 1.61 | 1.84 | 1.96 | 1.95 | 1.79 | 1.41 | 0 |
(2)在同一平面直角坐标系![]() 中,描出补全后的表中各组数值所对应的点
中,描出补全后的表中各组数值所对应的点![]() ,
,![]() ,并画出函数
,并画出函数![]() ,
,![]() 的图象;
的图象;
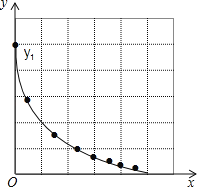
(3)结合函数图象,解决问题:
①当![]() ,
,![]() 的长都大于
的长都大于![]() 时,
时,![]() 长度的取值范围约是 ;
长度的取值范围约是 ;
②点![]() ,
,![]() ,
,![]() 能否在以
能否在以![]() 为圆心的同一个圆上? (填“能”或“否”)
为圆心的同一个圆上? (填“能”或“否”)