题目内容
12.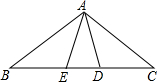 如图,△ABC中,D、E是BC边上的点,∠BAD=∠BDA,∠CAE=∠CEA,∠DAE=$\frac{1}{3}$∠BAC,则∠BAC的度数为108°.
如图,△ABC中,D、E是BC边上的点,∠BAD=∠BDA,∠CAE=∠CEA,∠DAE=$\frac{1}{3}$∠BAC,则∠BAC的度数为108°.
分析 设∠EAD=x,则∠BAE+∠CAD=2x,再根据∠BAD=∠BDA,∠CAE=∠CEA可知,∠BAD=∠DAE+∠BAE=x+∠BAE,∠CEA=∠CAE=∠DAE+∠CAD=x+∠CAD,再由三角形内角和定理即可得出结论.
解答 解:∵∠DAE=$\frac{1}{3}$∠BAC,
∴设∠EAD=x,则∠BAE+∠CAD=2x.
∵∠BAD=∠BDA,∠CAE=∠CEA,
∴∠BAD=∠DAE+∠BAE=x+∠BAE,∠CEA=∠CAE=∠DAE+∠CAD=x+∠CAD,
在△ADE中,
∵∠DAE+∠AED+∠ADE=180°,
∴x+x+∠CAD+x+∠BAE=180°,即5x=180°,解得x=36°,
∴∠BAC=3x=108°.
故答案为:108°.
点评 本题考查的是三角形内角和定理,熟知三角形内角和是180°是解答此题的关键.

练习册系列答案
 名师导航单元期末冲刺100分系列答案
名师导航单元期末冲刺100分系列答案 名校名卷单元同步训练测试题系列答案
名校名卷单元同步训练测试题系列答案
相关题目
3.点(x,0)的位置是( )
| A. | 原点 | B. | x轴上 | C. | y轴上 | D. | 任一象限内 |
20.能判定四边形ABCD为平行四边形的题设是( )
| A. | AB∥CD,AD=BC | B. | AB=CD,AD=BC | C. | ∠A=∠B,∠C=∠D | D. | AB=AD,CB=CD |
1.已知3xn+m-1-4yn-2=5是关于x和y的二元一次方程,则m2-n的值为( )
| A. | 1 | B. | 2 | C. | -2 | D. | -1 |
 如图所示,A、B两地位于某高速铁路沿线(直线)的两侧.
如图所示,A、B两地位于某高速铁路沿线(直线)的两侧.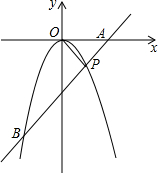 如图,抛物线y=ax2(a≠0)与直线AB交于点P(4,-4),连接OP,则OP=AP,求二次函数的解析式及抛物线与直线AB另一个交点B的坐标.
如图,抛物线y=ax2(a≠0)与直线AB交于点P(4,-4),连接OP,则OP=AP,求二次函数的解析式及抛物线与直线AB另一个交点B的坐标.