题目内容
6.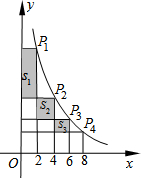 如图,在函数y=$\frac{24}{x}$(x>0)的图象上有点P1,P2,P3,…,Pn,Pn+1,点P1的横坐标为2,且后面每个点的横坐标与它前面相邻点的横坐标的差都是2,过点P1,P2,P3,…,Pn,Pn+1,分别作x轴、y轴的垂线段,构成若干个矩形,将图中阴影部分的面积从左至右依次记为S1,S2,S3,…,Sn,则S1=12;Sn=$\frac{24}{n(n+1)}$.
如图,在函数y=$\frac{24}{x}$(x>0)的图象上有点P1,P2,P3,…,Pn,Pn+1,点P1的横坐标为2,且后面每个点的横坐标与它前面相邻点的横坐标的差都是2,过点P1,P2,P3,…,Pn,Pn+1,分别作x轴、y轴的垂线段,构成若干个矩形,将图中阴影部分的面积从左至右依次记为S1,S2,S3,…,Sn,则S1=12;Sn=$\frac{24}{n(n+1)}$.
分析 求出P1、P2、P3、P4…的纵坐标,从而可计算出S1、S2、S3、S4…的高,进而求出S1、S2、S3、S4…,从而得出Sn的值.
解答 解:当x=2时,P1的纵坐标为12,
当x=4时,P2的纵坐标为6,
当x=6时,P3的纵坐标为4,
当x=8时,P4的纵坐标为3
…
则S1=2×(12-6)=12=$\frac{24}{1×(1+1)}$;
S2=2×(6-4)=4=$\frac{24}{2×(2+1)}$;
S3=2×(4-3)=2=$\frac{24}{3×(3+1)}$;
…
Sn=$\frac{24}{n(n+1)}$.
故答案为:12;$\frac{24}{n(n+1)}$.
点评 此题考查了反比例函数图象上点的坐标特征,根据坐标求出各阴影的面积表达式是解题的关键.

练习册系列答案
 口算题天天练系列答案
口算题天天练系列答案
相关题目
16.己知反比例函数y=$\frac{k}{x}$(k≠0)的图象经过点P(2,-3),则这个函数的图象位于( )
| A. | 第一、三象限 | B. | 第二、四象限 | C. | 第一、二象限 | D. | 第三、四象限 |
1.直线y=$\frac{1}{2}$x+b与直线y=-2x+2的交点不可能在( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
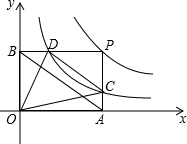 如图,P(m,n)是函数y=$\frac{6}{x}$(x>0)的图象上的一个动点,过点P分别作PA⊥x轴于A、PB⊥y轴于B,PA、PB分别与函数y=$\frac{2}{x}$(x>0)的图象交于点C、D,连接AB、CD.
如图,P(m,n)是函数y=$\frac{6}{x}$(x>0)的图象上的一个动点,过点P分别作PA⊥x轴于A、PB⊥y轴于B,PA、PB分别与函数y=$\frac{2}{x}$(x>0)的图象交于点C、D,连接AB、CD.
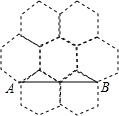 蜂巢的构造非常美丽、科学,如图是由7个形状、大小完全相同的正六边形组成的网络,正六边形的顶点称为格点,△ABC的顶点都在格点上.设定AB边如图所示,则△ABC是直角三角形的个数有10.
蜂巢的构造非常美丽、科学,如图是由7个形状、大小完全相同的正六边形组成的网络,正六边形的顶点称为格点,△ABC的顶点都在格点上.设定AB边如图所示,则△ABC是直角三角形的个数有10.