题目内容
如图,在平面直角坐标系中,点A的坐标为(1,1),OA=AC,∠OAC=90°,点D为x轴上一动点,以AD为边在AD的右侧作正方形ADEF.
(1)当点D在线段OC上时(不与点O、C重合),则线段CF与OD之间的数量关系为 ;位置关系为 .
(2)当点D在线段OC的延长线上时,(1)中的结论是否成立?若成立,请说明理由;若不成立,请举一反例;
(3)设D点坐标为(t,0)当D点从O点运动到C点时,用含t的代数式表示E点坐标,并直接写出E点所经过的路径长.

(1)当点D在线段OC上时(不与点O、C重合),则线段CF与OD之间的数量关系为
(2)当点D在线段OC的延长线上时,(1)中的结论是否成立?若成立,请说明理由;若不成立,请举一反例;
(3)设D点坐标为(t,0)当D点从O点运动到C点时,用含t的代数式表示E点坐标,并直接写出E点所经过的路径长.

考点:四边形综合题
专题:
分析:(1)比较两个线段的大小,首先要表示出两条线段.连接CF,发现△ODA与△CFA非常相近,进而考虑是否全等.通过同角的余角相等可得∠OAD=∠CAF,由正方形性质可得AD=AF,再由已知OA=OC易证,即得两三角形全等,而OD=CF.位置关系由图易猜想为垂直,即考虑∠FCO是否等于90°.∠FCO=∠FCA+∠ACO,由△ODA≌△CFA,所以∠FCA=∠DOA,即∠FCO=∠FCA+∠ACO=∠DOA+∠ACO(Rt△OAC的两个锐角的和),故∠FCO=90°,猜想成立.
(2)分析本问,首先要表示出该情形.在备用图中x轴上C的右方任取一点,按题目要求构造正方形ADEF,连接CF,观察发现(1)的结论好像在这种情形下依然成立.利用(1)的方法证明,结论易得.
(3)求某点坐标首先要做关于x轴、y轴的平行线将其横纵坐标表示出来,如图发现情况分为t<1,t=1,t>1三种.分别讨论利用全等三角形代换所求边长易得结论.注意边长都是正数,而若点出现在三四象限,纵坐标的值要为边长的相反数.后半问的经过路径长首先要清楚点的运动路径.根据上半问的坐标可以分析出点运动的轨迹,再利用所求知识求得.
(2)分析本问,首先要表示出该情形.在备用图中x轴上C的右方任取一点,按题目要求构造正方形ADEF,连接CF,观察发现(1)的结论好像在这种情形下依然成立.利用(1)的方法证明,结论易得.
(3)求某点坐标首先要做关于x轴、y轴的平行线将其横纵坐标表示出来,如图发现情况分为t<1,t=1,t>1三种.分别讨论利用全等三角形代换所求边长易得结论.注意边长都是正数,而若点出现在三四象限,纵坐标的值要为边长的相反数.后半问的经过路径长首先要清楚点的运动路径.根据上半问的坐标可以分析出点运动的轨迹,再利用所求知识求得.
解答:解:
(1)相等; 垂直.
(2)(1)中结论依然成立,即OD=CF,OD⊥CF
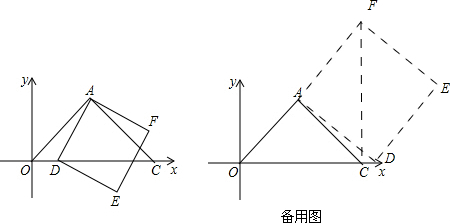
在x轴C点右方任取一点D,连接AD,并以AD为一边如图建立正方形ADEF,连接CF.
∵∠OAC=90°,∠DAF=90°
∴∠OAC=∠DAF
∴∠OAD=∠OAC+∠CAD=∠DAF+∠CAD=∠CAF
在△OAD和△CAF中
∴△OAD≌△CAF
∴OD=CF,∠AOD=∠ACF
∴∠OCF=∠OCA+∠ACF=∠OCA+∠AOC
在Rt△OAC中
∵∠OCA+∠AOC=90°
∴∠OCF=90°
∴OD⊥CF
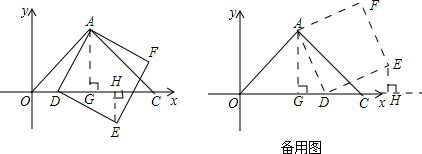
(3)过点A作AG⊥x轴于G,过点E作EH⊥x轴于H
∵OA=CA
∴OG=CG
∵A的坐标为(1,1)
∴OG=1,AG=1,OC=2
当D在线段OG上,如左图,此时t<1,则DG=1-t
在Rt△ADG中
∵∠DAG+∠ADG=90°,∠ADG+∠HDE=90°
∴∠DAG=∠HDE
在△ADG和△DEH中
∴△ADG≌△DEH
∴HE=DG=1-t,DH=AG=1
∴OH=OD+DH=t+1
∴E点坐标为(t+1,-(1-t)),即(t+1,t-1)
当D与G点重合,E点与C点重合,即E点坐标为(2,0).由此时t=1,所以E点坐标也为(t+1,t-1)
当D在线段GC上,如右图,此时t>1,则DG=t-1
∵∠ADE=90°
∴∠ADG+∠HDE=90°
在Rt△ADG中
∵∠DAG+∠ADG=90°
∴∠DAG=∠HDE
在△ADG和△DEH中
∴△ADG≌△DEH
∴HE=DG=t-1,DH=AG=1
∴OH=OD+DH=t+1
∴E点坐标为(t+1,t-1)
综上所述,E点坐标为(t+1,t-1),0≤t≤2
由(t+1,t-1)在y=x-2上,则E点由(1,-1)直线运动到(3,1),作关于x轴、y轴的平行线,利用勾股定理易得,E点运动的距离为2
.
(1)相等; 垂直.
(2)(1)中结论依然成立,即OD=CF,OD⊥CF

在x轴C点右方任取一点D,连接AD,并以AD为一边如图建立正方形ADEF,连接CF.
∵∠OAC=90°,∠DAF=90°
∴∠OAC=∠DAF
∴∠OAD=∠OAC+∠CAD=∠DAF+∠CAD=∠CAF
在△OAD和△CAF中
|
∴△OAD≌△CAF
∴OD=CF,∠AOD=∠ACF
∴∠OCF=∠OCA+∠ACF=∠OCA+∠AOC
在Rt△OAC中
∵∠OCA+∠AOC=90°
∴∠OCF=90°
∴OD⊥CF
(3)过点A作AG⊥x轴于G,过点E作EH⊥x轴于H

∵OA=CA
∴OG=CG
∵A的坐标为(1,1)
∴OG=1,AG=1,OC=2
当D在线段OG上,如左图,此时t<1,则DG=1-t
在Rt△ADG中
∵∠DAG+∠ADG=90°,∠ADG+∠HDE=90°
∴∠DAG=∠HDE
在△ADG和△DEH中
|
∴△ADG≌△DEH
∴HE=DG=1-t,DH=AG=1
∴OH=OD+DH=t+1
∴E点坐标为(t+1,-(1-t)),即(t+1,t-1)
当D与G点重合,E点与C点重合,即E点坐标为(2,0).由此时t=1,所以E点坐标也为(t+1,t-1)
当D在线段GC上,如右图,此时t>1,则DG=t-1
∵∠ADE=90°
∴∠ADG+∠HDE=90°
在Rt△ADG中
∵∠DAG+∠ADG=90°
∴∠DAG=∠HDE
在△ADG和△DEH中
|
∴△ADG≌△DEH
∴HE=DG=t-1,DH=AG=1
∴OH=OD+DH=t+1
∴E点坐标为(t+1,t-1)
综上所述,E点坐标为(t+1,t-1),0≤t≤2
由(t+1,t-1)在y=x-2上,则E点由(1,-1)直线运动到(3,1),作关于x轴、y轴的平行线,利用勾股定理易得,E点运动的距离为2
| 2 |
点评:本题的难度不是很高,学生只要清晰概念很容易得到前两问的结论.但第三问中注意边长都是正数,而若点出现在三四象限,纵坐标的值要为边长的相反数,这里是易错点.另外后半问的求经过路径长首先要清楚的是点的运动路径.这要根据上半问的坐标分析得出,方法既横坐标如何变换(不含字母)得到纵坐标,以确定点的运动方程,此类考点不常出现,须特殊留意.最后在坐标系中求点到点的距离一般都是分别作x轴、y轴的平行线构造直角三角形,进而利用勾股定理求得,这类常规题也许多加练习.

练习册系列答案
相关题目
计算
-
的结果是( )
| 48 |
| 27 |
A、
| ||
B、-
| ||
C、
| ||
| D、1 |
下列各式中,是二次根式的有( )
①
; ②
; ③
; ④
; ⑤
(x≤3); ⑥
(x>0);
⑦
; ⑧
; ⑨
(ab≥0); ⑩
(ab>0).
①
| 7 |
| -3 |
| 3 | 10 |
|
| 3-x |
| -2x |
⑦
| (a-3)2 |
| -x2-1 |
| ab |
|
| A、4个 | B、5个 | C、6个 | D、7个 |
计算-(a2b)3+2a2b•(-3a2b)2的结果为( )
| A、-17a6b3 |
| B、-18a6b3 |
| C、17a6b3 |
| D、18a6b3 |