题目内容
用适当方法解下列方程:
(1)2x2-5x-3=0
(2)(2x-3)2-2(2x-3)-3=0
(3)(2x-1)2=9
(4)3x2+5(2x+1)=0.
解:(1)因式分解得(x-3)(2x+1)=0,
即x-3=0或2x+1=0,
解得x1=3,x2=- ;
;
(2)设2x-3=t,则方程即可变形为t2-2t-3=0,
(t+1)(t-3)=0,
解得t=-1或3,
即2x-3=-1或3,
解得x1=1,x2=3;
(3)开平方,得2x-1=±3,
解得x1=2,x2=-1;
(4)整理得3x2+10x+5=0,
∵a=3,b=10,c=5,△=b2-4ac=100-60=40,
∴x= =
=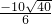 =
=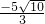 ,
,
∴x1= ,x2=
,x2= .
.
分析:(1)先因式分解,再求出x即可;
(2)先设2x-3=t,则方程即可变形为t2-2t-3=0,解方程即可求得t即得出x值;
(3)用直接开平方法求出2x-1的值,再得出x即可;
(4)先去括号,再找出a,b,c,再求出△,代入求根公式x= 计算即可.
计算即可.
点评:本题考查了一元二次方程的解法,解一元二次方程的方法有:直接开平方法、公式法、因式分解法以及换元法.
即x-3=0或2x+1=0,
解得x1=3,x2=-
 ;
;(2)设2x-3=t,则方程即可变形为t2-2t-3=0,
(t+1)(t-3)=0,
解得t=-1或3,
即2x-3=-1或3,
解得x1=1,x2=3;
(3)开平方,得2x-1=±3,
解得x1=2,x2=-1;
(4)整理得3x2+10x+5=0,
∵a=3,b=10,c=5,△=b2-4ac=100-60=40,
∴x=
 =
=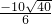 =
=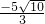 ,
,∴x1=
 ,x2=
,x2= .
.分析:(1)先因式分解,再求出x即可;
(2)先设2x-3=t,则方程即可变形为t2-2t-3=0,解方程即可求得t即得出x值;
(3)用直接开平方法求出2x-1的值,再得出x即可;
(4)先去括号,再找出a,b,c,再求出△,代入求根公式x=
 计算即可.
计算即可.点评:本题考查了一元二次方程的解法,解一元二次方程的方法有:直接开平方法、公式法、因式分解法以及换元法.

练习册系列答案
相关题目