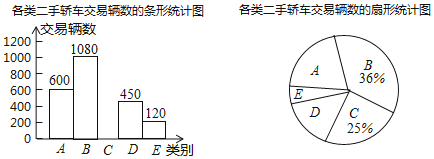
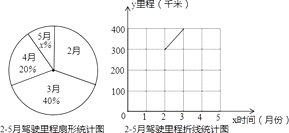
题目内容
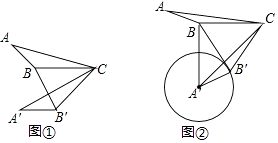
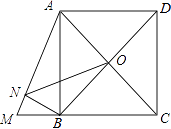
【题目】如图,正方形ABCD的边长为4,延长CB至M,使BM=2,连接AM,BN⊥AM于N,O是AC、BD的交点,连接ON,则ON的长为 
【答案】![]()
【解析】解:∵AB=4,BM=2,
∴AM= ![]() =2
=2 ![]() ,
,
∵∠ABM=90°,BN⊥AM,
∴△ABN∽△BNM∽△AMB,
∴AB2=AN×AM,BM2=MN×AM,
∴AN= ![]() ,MN=
,MN= ![]() ,
,
∵AB=4,CD=4,
∴AC=4 ![]() ,
,
∴AO=2 ![]() ,
,
∵ ![]() =
= ![]() =
= ![]() ,且∠CAM=∠NAO
,且∠CAM=∠NAO
∴△AON∽△AMC,
∴ ![]() =
= ![]() ,即
,即 ![]() =
= ![]() ,
,
∴ON= ![]() .
.
所以答案是: ![]() .
.
【考点精析】掌握勾股定理的概念和正方形的性质是解答本题的根本,需要知道直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2;正方形四个角都是直角,四条边都相等;正方形的两条对角线相等,并且互相垂直平分,每条对角线平分一组对角;正方形的一条对角线把正方形分成两个全等的等腰直角三角形;正方形的对角线与边的夹角是45o;正方形的两条对角线把这个正方形分成四个全等的等腰直角三角形.

练习册系列答案
相关题目
【题目】二次函数y=ax2+bx+c(a,b,c为常数,且a≠0)中的x与y的部分对应值如表
x | ﹣1 | 0 | 1 | 3 |
y | ﹣1 | 3 | 5 | 3 |
下列结论:
①ac<0;
②当x>1时,y的值随x值的增大而减小.
③3是方程ax2+(b﹣1)x+c=0的一个根;
④当﹣1<x<3时,ax2+(b﹣1)x+c>0.
其中正确的结论是 .