题目内容
有长、宽、高分别为48cm、36cm、24cm的长方体,若要将它锯成若干个大小相同的小正方体,问至少能锯成 块.
考点:约数与倍数
专题:
分析:首先求出48、36和24的最大公因数,以三个数最大公因数为边长的小正方形就是所要锯成的小正方形,即可算出小正方形的数量.
解答:解:出48、36和24的最大公因数是12,
即锯成的小正方形的边长为12cm,
长方体的体积为48×36×24=41472cm3,
小正方形的体积为12×12×12=1728cm3,
小正方形的个数n=
=24(块).
故答案为:24.
即锯成的小正方形的边长为12cm,
长方体的体积为48×36×24=41472cm3,
小正方形的体积为12×12×12=1728cm3,
小正方形的个数n=
| 41472 |
| 12×12×12 |
故答案为:24.
点评:本题主要考查了约数与倍数的知识点,解答本题的关键是找出48、36和24的最大公因数,此题难度不大.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
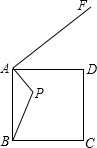 已知点P是边长为5的正方形ABCD内一点,且AP=2,AF⊥AP,垂足是点A,若在射线AF上找一点M,使以点A,M,D为顶点的三角形与△ABP相似,则AM为( )
已知点P是边长为5的正方形ABCD内一点,且AP=2,AF⊥AP,垂足是点A,若在射线AF上找一点M,使以点A,M,D为顶点的三角形与△ABP相似,则AM为( )| A、2 | ||
| B、5 | ||
C、2或
| ||
D、2或
|
 钓鱼岛及其附属daoyu是我国的固有领土,台湾保diao人士组团前往钓鱼岛,宣示主权.当保diao船航行至海面B处时(如图),测得钓鱼岛位于正北方向20海里的C处,为了防止日本海巡警干扰,就请求我A处的海监船前往C处护航.已知C处位于A处的北偏东45°的方向上,A位于B的北偏西30°的方向上.
钓鱼岛及其附属daoyu是我国的固有领土,台湾保diao人士组团前往钓鱼岛,宣示主权.当保diao船航行至海面B处时(如图),测得钓鱼岛位于正北方向20海里的C处,为了防止日本海巡警干扰,就请求我A处的海监船前往C处护航.已知C处位于A处的北偏东45°的方向上,A位于B的北偏西30°的方向上.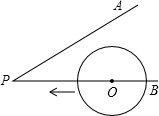 如图,∠APB=30°,点O是射线PB上的一点,OP=5cm,若以点O为圆心,半径为1.5cm的⊙O沿BP方向移动,当⊙O与PA相切时,圆心O移动的距离为
如图,∠APB=30°,点O是射线PB上的一点,OP=5cm,若以点O为圆心,半径为1.5cm的⊙O沿BP方向移动,当⊙O与PA相切时,圆心O移动的距离为
 如图,在等腰△ABC的两腰AB、BC上分别取点D和E,使DB=DE,此时恰有∠ADE=
如图,在等腰△ABC的两腰AB、BC上分别取点D和E,使DB=DE,此时恰有∠ADE=


