Question

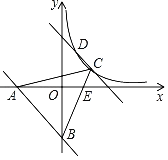
【题目】如图所示，一次函数y＝﹣x﹣6与x轴，y轴分别交于点A，B将直线AB沿y轴正方向平移与反比例函数y＝（x＞0）的图象分别交于点C，D，连接BC交x轴于点E，连接AC，已知BE＝3CE，且S△ABE＝27．

（1）求直线AC和反比例函数的解析式；

（2）连接AD，求△ACD的面积．

Answer 1

【答案】（1）y＝，y＝x+；（2）12

【解析】

（1）先求得y＝﹣x﹣6与坐标轴的交点，从而可得点A和点B的坐标，进而求得AE和OE的长；过C作CN⊥x轴于N，由平行线截线段成比例定理可得比例式，从而求得EN、CN和ON，则点C的坐标可得；从而反比例函数的解析式可得；设直线AC的解析式为y＝kx+b（k≠0），用待定系数法即可求得答案；

（2）根据题意设直线CD的解析式为y＝﹣x+b1，将点C（4，2）代入，解得b1的值，则CD的解析式可得；将直线CD和反比例函数解析式联立可解得点D的坐标；过D作DM∥y轴交AC于M，利用关系式S△ACD＝S△ADM+S△CDM可求得答案．

解：（1）在y＝﹣x﹣6中，当x＝0时，y＝﹣6；当y＝0时，x＝﹣6，

∴A（﹣6，0），B（0，﹣6），

∴OB＝OA＝6，又S△ABE＝27，

∴OB×AE＝27，

∴AE＝9，OE＝3，

过C作CN⊥x轴于N，

则CN∥OB，

又∵BE＝3CE，

∴，

∴EN＝1，CN＝2，ON＝4，

∴C（4，2），

∴反比例函数的解析式为y＝，

设直线AC的解析式为y＝kx+b（k≠0），将A（﹣6，0），C（4，2）代入得：

，

解得：，

∴直线AC的解析式为y＝x+；

（2）根据题意设直线CD的解析式为y＝﹣x+b1，将点C（4，2）代入得：

﹣4+b1＝2，

∴b1＝6，

∴直线CD的解析式为y＝﹣x+6，

将直线CD和反比例函数解析式联立得：，

解得：或，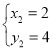

∴D（2，4），

过D作DM∥y轴交AC于M，则M（2，1.6），

∴S△ACD＝S△ADM+S△CDM

＝DM|xM﹣xA|+DM|xC﹣xM|

＝DM|xC﹣xA|

＝×（4﹣1.6）×|4﹣（﹣6）|

＝12．