题目内容
 14、已知A,C,B在同一条直线上,△ACE,△BCF都是等边三角形,BE交CF于N,AF交CE于M,MG⊥CN,垂足为G.求证:CG=NG.
14、已知A,C,B在同一条直线上,△ACE,△BCF都是等边三角形,BE交CF于N,AF交CE于M,MG⊥CN,垂足为G.求证:CG=NG.分析:先证△ACF与△ECB全等,得到∠AFC=∠ABE,再证△FMC≌△BCN得到MC=MN,有条件MG垂直于NC而得到结论.
解答:证明:∵△ACE,△BCF都是等边三角形,
∴AC=EC,FC=BC,∠ACE=∠BCF=60°,
∴∠ECN=60°,∠BCE=∠ACF,
∴三角形ACF与三角形ECB全等,
∴∠AFC=∠ABE,
∴△FMC≌△BCN,
∴MN=CN,
∵∠ECN=60°,
∴MC=MN,
∵MG⊥NC,
∴GC=GN.
∴AC=EC,FC=BC,∠ACE=∠BCF=60°,
∴∠ECN=60°,∠BCE=∠ACF,
∴三角形ACF与三角形ECB全等,
∴∠AFC=∠ABE,
∴△FMC≌△BCN,
∴MN=CN,
∵∠ECN=60°,
∴MC=MN,
∵MG⊥NC,
∴GC=GN.
点评:本题考查了等边三角形的性质,通过两次全等得到MC=MN,通过MG垂直于NC得到结论.

练习册系列答案
相关题目
 5、如图,已知B、C、E在同一直线上,且CD∥AB,若∠A=75°,∠B=40°,则∠ACE为( )
5、如图,已知B、C、E在同一直线上,且CD∥AB,若∠A=75°,∠B=40°,则∠ACE为( )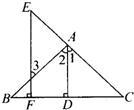 21、补全下列证明过程及括号内的推理依据:
21、补全下列证明过程及括号内的推理依据: 如图,已知B、C、E在同一直线上,且CD∥AB,若∠A=105°,∠B=40°,则∠ACE为
如图,已知B、C、E在同一直线上,且CD∥AB,若∠A=105°,∠B=40°,则∠ACE为