题目内容
1.如图,已知M是线段AB的中点,N是AM上一点且满足MN=2AN,P为BN的中点,则AB=( )MP.
| A. | 9 | B. | 10 | C. | 11 | D. | 12 |
分析 设AN=x,MN=2x,于是得到AM=3x,由M是线段AB的中点,得到AB=2AM=6x,求得BN=5x,根据P为BN的中点,得到PN=$\frac{1}{2}$BN=2.5x,求得PM=PN-MN=0.5x,于是得到结论.
解答 解:∵MN=2AN,
设AN=x,MN=2x,
∴AM=3x,
∵M是线段AB的中点,
∴AB=2AM=6x,
∴BN=5x,
∵P为BN的中点,
∴PN=$\frac{1}{2}$BN=2.5x,
∴PM=PN-MN=0.5x,
∴AB=12MP,
故选D.
点评 本题考查的是两点间的距离,熟知各线段之间的和、差及倍数关系是解答此题的关键.

练习册系列答案
 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案 应用题作业本系列答案
应用题作业本系列答案
相关题目
11.实数a,b,c满足a2+6b=-17,b2+8c=-23,c2+2a=14,则a+b+c的值是( )
| A. | -6 | B. | -7 | C. | -8 | D. | -9 |
12. 如图,△ABC和△EFC都是等边三角形,AD是△ABC的高,AB=4,若点E在直线AD上运动,连接DF,则在点E运动过程中,线段DF的最小值是( )
如图,△ABC和△EFC都是等边三角形,AD是△ABC的高,AB=4,若点E在直线AD上运动,连接DF,则在点E运动过程中,线段DF的最小值是( )
 如图,△ABC和△EFC都是等边三角形,AD是△ABC的高,AB=4,若点E在直线AD上运动,连接DF,则在点E运动过程中,线段DF的最小值是( )
如图,△ABC和△EFC都是等边三角形,AD是△ABC的高,AB=4,若点E在直线AD上运动,连接DF,则在点E运动过程中,线段DF的最小值是( )| A. | 1 | B. | 2 | C. | $\frac{\sqrt{3}}{2}$ | D. | $\frac{2\sqrt{3}}{3}$ |
16.若m是任意实数,则点A(m2+1,-4)在( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
10.△ABC中,∠A=25°,∠B=87°,则∠C=( )
| A. | 58° | B. | 68° | C. | 78° | D. | 87° |
11.下列四个方程中,是一元一次方程的是( )
| A. | 2x-y=1 | B. | x 2-3 x+1=0 | C. | x=7 | D. | $\frac{2}{x}$=1 |
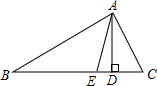 如图所示,已知在△ABC中,AD⊥BC于D,AE平分∠BAC,若∠B=28°,∠DAE=16°,求∠C的度数.
如图所示,已知在△ABC中,AD⊥BC于D,AE平分∠BAC,若∠B=28°,∠DAE=16°,求∠C的度数.