题目内容
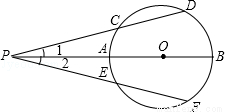
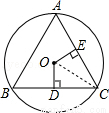
如图，在⊙O中，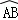
与
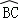相等，OD⊥BC，OE⊥AC，垂足分别为D、E，且OD=OE，那么△ABC是什么三角形，为什么？
等边三角形
【解析】
试题分析：根据圆心角、弧、弦的关系由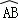
=
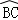得到AB=BC，再由OD⊥BC，OE⊥AC，根据垂径定理和垂直的定义得到CE=
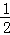AC，CD=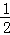BC，∠ODC=∠OEC=90°利用三角形全等的判定方法可得到Rt△ODC≌Rt△OEC（HL），则CD=CE，于是有BC=AC，则AB=AC=CB，即可得到△ABC为等边三角形．
【解析】
△ABC为等边三角形．理由如下：
连OC，
∵
=
，
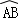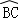∴AB=BC，
∵OD⊥BC，OE⊥AC，
∴CE=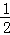AC，CD=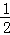BC，∠ODC=∠OEC=90°
∵在Rt△ODC和Rt△OEC中，
，
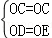∴Rt△ODC≌Rt△OEC（HL）
∴CD=CE，
∴BC=AC，
∴AB=AC=CB，
∴△ABC为等边三角形．
练习册系列答案
相关题目
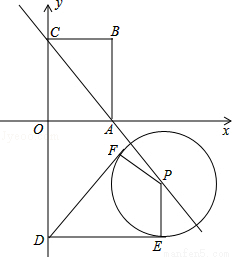
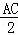，过点D作动圆P的两条切线与动圆P分别相切于点E、F．请探求在动圆P中是否存在面积最小的四边形DEPF？若存在，请求出最小面积S的值；若不存在，请说明理由．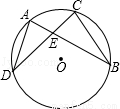
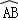与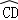
的长度，并证明你的结论；
