Question

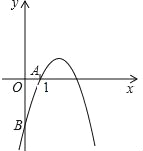
【题目】如图，抛物线y＝﹣x2+5x+n经过点A(1，0)，与y轴交于点B．

(1)求抛物线的解析式；

(2)P是y轴正半轴上一点，且△PAB是以AB为腰的等腰三角形，试求P点坐标．

Answer 1

【答案】（1）；（2）（0，）或（0，4）．

【解析】

试题（1）将A点的坐标代入抛物线中，即可得出二次函数的解析式；

（2）本题要分两种情况进行讨论：①PB=AB，先根据抛物线的解析式求出B点的坐标，即可得出OB的长，进而可求出AB的长，也就知道了PB的长，由此可求出P点的坐标；

②PA=AB，此时P与B关于x轴对称，由此可求出P点的坐标．

试题解析：（1）∵抛物线经过点A（1，0），∴，∴；

（2）∵抛物线的解析式为，∴令，则，∴B点坐标（0，﹣4），AB=，

①当PB=AB时，PB=AB=，∴OP=PB﹣OB=．∴P（0，），

②当PA=AB时，P、B关于x轴对称，∴P（0，4），因此P点的坐标为（0，）或（0，4）．