题目内容
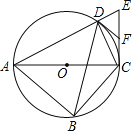
【题目】如图,△ABC是⊙O的内接三角形,直径AB=10.sinA=![]() ,点D为线段AC上一动点(不运动至端点A、C),作DF⊥AB于F,连结BD,井延长BD交⊙O于点H,连结CF.
,点D为线段AC上一动点(不运动至端点A、C),作DF⊥AB于F,连结BD,井延长BD交⊙O于点H,连结CF.
(1)当DF经过圆心O时,求AD的长;
(2)求证:△ACF∽△ABD;
(3)求CFDH的最大值.

【答案】(1)![]() (2)证明见解析(3)当x=4时,CFDH的最大值为
(2)证明见解析(3)当x=4时,CFDH的最大值为![]()
【解析】
(1)由AB是直径知∠ACB=90°,依据三角函数求出BC=6,由勾股定理求出AC=8,由AB⊥DE知∠AFD=∠ACB=90°,结合∠A为公共角可证△ADF∽△ABC,得出对应边成比例,即可求出AD的长;
(2)由△ADF∽△ABC知![]() ,结合∠A为△ACF和△ABD的公共角可证△ACF∽△ABD;
,结合∠A为△ACF和△ABD的公共角可证△ACF∽△ABD;
(3)连接CH,先证△ACH∽△HCD得出比例式,即CFDH=CDAF,再设AD=x,则CD=8﹣x,AF=![]() x,从而得出CFDH=﹣
x,从而得出CFDH=﹣![]() (x﹣4)2+
(x﹣4)2+![]() ,利用二次函数的性质求解可得.
,利用二次函数的性质求解可得.
(1)当DF经过圆心O时,AF=OA=5,
∵AB为直径,AB=10,
∴∠ACB=90°,
∴sinA=![]() ,
,
∴BC=6,
由勾股定理得:![]() ,
,
∵AB⊥DE,
∴∠AFD=∠ACB=90°,
∵∠A=∠A,
∴△ADF∽△ABC,
∴![]() ,
,
∴![]() ;
;
(2)证明:由(1)得:△ADF∽△ABC,
∴![]() ,即
,即![]() ,
,
又∵∠A为△ACF和△ABD的公共角,
∴△ACF∽△ABD;
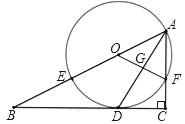
(3)连接CH,如图所示:
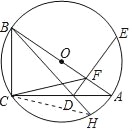
由(2)知△ACF∽△ABD,
∴∠ABD=∠ACF,
∵∠ABD=∠ACH,
∴∠ACH=∠ACF,
又∵∠CAF=∠H,
∴△ACH∽△HCD,
∴![]() ,即CFDH=CDAF,
,即CFDH=CDAF,
设AD=x,则CD=8﹣x,AF=![]() x,
x,
∴CFDH=![]() x(8﹣x)=﹣
x(8﹣x)=﹣![]() x2+
x2+![]() x=﹣
x=﹣![]() (x﹣4)2+
(x﹣4)2+![]() ,
,
∴当x=4时,CFDH的最大值为![]() .
.

【题目】某校计划购进甲、乙两种规格的书架,经市场调查发现有线上和线下两种购买方式,具体情况如下表:
规格 | 线下 | 线上 | ||
单价(元/个) | 运费(元/个) | 单价(元/个) | 运费(元/个) | |
甲 | 240 | 0 | 210 | 20 |
乙 | 300 | 0 | 250 | 30 |
(1)如果在线下购买甲、乙两种书架共30个,花费8280元,求甲、乙两种书架各购买了多少个?
(2)如果在线上购买甲、乙两种书架共30个,且购买乙种书架的数量不少于甲种书架的3倍,请求出花费最少的购买方案及花费.