题目内容
如图,在Rt△ABC中,∠ACB=90°,D、E分别为AB,AC边上的中点,连接DE,将△ADE绕点E旋转180°得到△CFE,连接AF,AC.
(1)求证:四边形ADCF是菱形;
(2)若BC=8,AC=6,求四边形ABCF的周长.

(1)证明:∵将△ADE绕点E旋转180°得到△CFE,
∴AE=CE,DE=EF,
∴四边形ADCF是平行四边形,
∵D、E分别为AB,AC边上的中点,
∴DE是△ABC的中位线,
∴DE∥BC,
∵∠ACB=90°,
∴∠AED=90°,
∴DF⊥AC,
∴四边形ADCF是菱形;
(2)解:在Rt△ABC中,BC=8,AC=6,
∴AB=10,
∵D是AB边上的中点,
∴AD=5,
∵四边形ADCF是菱形,
∴AF=FC=AD=5,
∴四边形ABCF的周长为8+10+5+5=28.

 尖子生新课堂课时作业系列答案
尖子生新课堂课时作业系列答案大庆油田某一年的石油总产量为4 500万吨,若用科学记数法表示应为( )吨.
|
| A. | 4.5×10﹣6 | B. | 4.5×106 | C. | 4.5×107 | D. | 4.5×108 |
在Rt△ABC中,∠C=90°,AC=12,BC=5,则sinA的值为( )
|
| A. |
| B. |
| C. |
| D. |
|
下列运算正确的是( )
|
| A. | (﹣2mn)2=4m2n2 | B. | y2+y2=2y4 | C. | (a﹣b)2=a2﹣b2 | D. | m2+m=m3 |
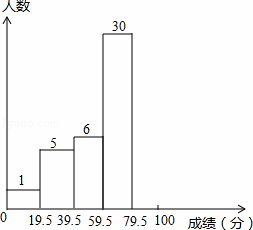
如图是某数学兴趣小组参加“奥数”后所得成绩绘制成的频数,频率分布表和频数分布直方图.请你根据图表提供的信息,解答下列问题(成绩取整数,满分为100分)
| 分组 | 0﹣19.5 | 19.5﹣39.5 | 39.5﹣59.5 | 59.5﹣79.5 | 79.5﹣100 | 合计 |
| 频数 | 1 | 5 | 6 | 30 | b | 50 |
| 频率 | 0.02 | a | 0.12 | 0.60 | 0.16 | 1 |
(1)频数、频率分布表中a= ,b= .
(2)补全频数分布直方图.
(3)若在80分以上的小组成员中选3人参加下一轮竞赛,小明本次竞赛的成绩为90分,他被选中的概率是多少?
(4)从该图中你还能获得哪些数学信息?(填写一条即可 )
)





 所对的圆心角∠AOB= ° ;
所对的圆心角∠AOB= ° ;