题目内容
如果抛物线y=（k+1）x2+x-k2+2与y轴的交点为（0，1），那么k的值是 ________．
1
分析：把交点为（0，1）代入抛物线解析式，解一元二次方程，即可解得k．
解答：∵抛物线y=（k+1）x2+x-k2+2与y轴的交点为（0，1），
∴-k2+2=1，
解得：k=±1，
∵k+1≠0，
∴k=1，
故答案为1．
点评：本题主要考查待定系数法求二次函数解析式的知识点，解答本题的关键是理解抛物线与y轴的交点问题，本题难度不大．
分析：把交点为（0，1）代入抛物线解析式，解一元二次方程，即可解得k．
解答：∵抛物线y=（k+1）x2+x-k2+2与y轴的交点为（0，1），
∴-k2+2=1，
解得：k=±1，
∵k+1≠0，
∴k=1，
故答案为1．
点评：本题主要考查待定系数法求二次函数解析式的知识点，解答本题的关键是理解抛物线与y轴的交点问题，本题难度不大．
练习册系列答案
阅读快车系列答案
相关题目
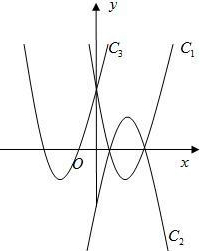如图示：己知抛物线C1，C2关于x轴对称，抛物线C1，C3关于y轴对称．如果抛物线C2的解析式是y=-如果抛物线经过点（2，3），（3，2）和（4，3），则抛物线的顶点是（ ）
| A、（2，3） | B、（3，2） | C、（4，3） | D、无法确定 |