题目内容
如图，已知：AD和BC相交于O，∠1=∠2，∠3=∠4．试判断AD和BC的关系，并说明理由．分析：根据ASA证△ABD≌△ACD，推出AB=AC，根据等腰三角形的性质得出即可．
解答：解：AD⊥BC，AD平分BC，
理由是：∵在△ABD和△ACD中
∴△ABD≌△ACD（ASA）
∴AB=AC，
∵∠1=∠2，
∴AD⊥BC，AD平分BC（等腰三角形三线合一性质）．
理由是：∵在△ABD和△ACD中
|
∴△ABD≌△ACD（ASA）
∴AB=AC，
∵∠1=∠2，
∴AD⊥BC，AD平分BC（等腰三角形三线合一性质）．
点评：本题考查了全等三角形的性质和判定，等腰三角形的性质和判定的应用，注意：等腰三角形顶角的平分线，底边上的高，底边上的中线互相重合．
练习册系列答案
相关题目
24、如图，已知正方形ABCD和正方形DEFG，点G在AD上．连接AE交FG于点M，连接CG并延长交AE于点N，
15、如图：已知：AD=AE，F是公共边，要让△ADF和△AEF全等只要给出条件：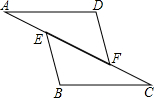
完成下面的证明过程：