题目内容
已知点D,E,F分别在△ABC的三边BC,CA,AB上,G为BE与CF的交点,并且BD=DC=CA=AF,AE=EC=BF,那么 的值等于________.
的值等于________.

分析:过E作AB的平行线交CF于M点,则EM是△AFC的中位线,M是中点,利用AAS求证△BFG≌△EMG然后得EM=BF,所以BG=GE,G是BE的中点,而D是BC的中点,所以DG是△BEC的中位线,然后即可得出答案.
解答:
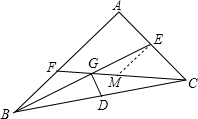 解:过E作AB的平行线交CF于M点,
解:过E作AB的平行线交CF于M点,∴EM是△AFC的中位线,M是中点,
∴EM=
 AF=BF,
AF=BF,∴△BFG≌△ENG,
∴BG=GE,即G是BE的中点,
又∵BD=DC,
∴DG是△BEC的中位线,
∴DG=
 CE=
CE= BD=
BD= BC.
BC.故答案为:

点评:此题主要考查学生对相似三角形的判定与性质,三角形中位线定理和全等三角形的判定与性质的理解和掌握,解得此题的关键是作“过E作AB的平行线交CF于M点”这一辅助线,然后求证出DG是△BEC的中位线,这是此题的突破点.

练习册系列答案
相关题目

 如图,在△ABC中,已知点D,E,F分别为BC,AD,CE的中点,且
如图,在△ABC中,已知点D,E,F分别为BC,AD,CE的中点,且 如图所示,在△ABC中,已知点D,E,F分别为BC,AD,BE的中点.且S△ABC=8cm2,则图中△CEF的面积=
如图所示,在△ABC中,已知点D,E,F分别为BC,AD,BE的中点.且S△ABC=8cm2,则图中△CEF的面积=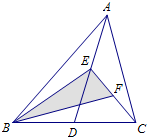 如图,△ABC中,已知点D、E、F分别为BC、AD、CE的中点,设△ABC的面积为S△ABC,△BEF的面积为S△BEF,则S△BEF:S△ABC=
如图,△ABC中,已知点D、E、F分别为BC、AD、CE的中点,设△ABC的面积为S△ABC,△BEF的面积为S△BEF,则S△BEF:S△ABC=