题目内容
(本题10分)某农场的一个开发商准备开发建设甲、乙两种户型的楼房,甲种楼房每套造价12万元,售价14.5万元;乙种楼房每套造价8万元,售价10万元,且它们的造价和售价始终不变.现准备建造甲、乙两种楼房共20套,所用资金不低于190万元,不高于200万元.
(1)该开发商有哪几种建造方案?
(2)该开发商采用哪种建造方案可获得最大利润?最大利润是多少?
(3)若用(2)中所求得的利润再次建造楼房,请直接写出获得最大利润的建造方案.
(1)有三种建造方案:建造甲种楼房8套,乙种楼房12套;建造甲种楼房9套,建造乙种楼房11套;建造甲种楼房l0套,乙种楼房10套
(2)建造甲种楼房10套,乙种楼房10套时,可获得最大利润,最大利润是45万元
(3)建造甲种楼房l套,乙种楼房4套时,可获得最大利润
【解析】
试题分析:首先设甲种楼房x套,则乙种楼房(20-x)套,根据资金列出不等式组,求出x的取值范围,然后根据x为非负整数求出方案;(2)根据每种方案求出最大利润.
试题解析:(1)设建造甲种楼房x套,乙种楼房(20-x)套.
根据题意得:190≤12x+8(20-x)≤200 解得7.5≤x≤10.
∵ x为非负整数,∴ x取8,9,l0
∴有三种建造方案:建造甲种楼房8套,乙种楼房12套;建造甲种楼房9套,建造乙种楼房11套;建造甲种楼房l0套,乙种楼房10套.
设总利润为w,则w=(14.5-12)x+(10-8)(20-x)=0.5x+40
∴当x取最大值时,利润最大,即建造甲种楼房10套,乙种楼房10套时,可获得最大利润,最大利润是45万元.
(3)建造甲种楼房l套,乙种楼房4套时,可获得最大利润
考点:不等式组的应用、一次函数的应用.

练习册系列答案
 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案
相关题目

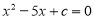 的一个根,则这个方程的另一个根是( )
的一个根,则这个方程的另一个根是( )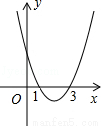
 (k≠0)在同一坐标系中的图象大致是( )
(k≠0)在同一坐标系中的图象大致是( )
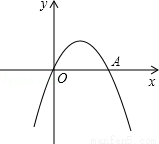

 ,
, ,mn这三个代数式间的等量关系吗?
,mn这三个代数式间的等量关系吗? D.5、12、13
D.5、12、13