Question

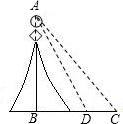
已知：如图，△ABC中，AB=3，∠BAC=120°，AC=1，D为AB延长线上一点，BD=1，点P在∠BAC的平分线上，且满足△PAD是等边三角形．
（1）求证：BC=BP；
（2）求点C到BP的距离．

Answer 1

（1）证明：如图，连接PC．
∵AC=1，BD=1，
∴AC=BD．
∵∠BAC=120°，AP平分∠BAC，
∴∠1=

1

2

∠BAC=60°．
∵△PAD是等边三角形，
∴PA=PD，∠D=60°．
∴∠1=∠D．
∴△PAC≌△PDB．
∴PC=PB，∠2=∠3．
∴∠2+∠4=∠3+∠4，∠BPC=∠DPA=60°．
∴△PBC是等边三角形，BC=BP．

（2）如图，作CE⊥PB于E，PF⊥AB于F．
∵AB=3，BD=1，
∴AD=4．
∴△PAD是等边三角形，PF⊥AB，
∴DF=

1

2

AD=2，PF=PD•sin60°=2

3

．
∴BF=DF-BD=1，
∴BP=

BF2+PF2

=

13

．
∴CE=BC•sin60°=BP•sin60°=

13

×

3

2

=

39

2

．
即点C至BP的距离等于

39

2

．