题目内容
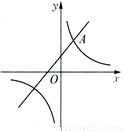
如图,一次函数y1=x+1的图像与反比例函数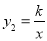 (k为常数,且k≠0)的图像都经过点A(m,2).
(k为常数,且k≠0)的图像都经过点A(m,2).
(1)求点A的坐标及反比例函数的表达式.
(2)结合图像直接比较:当x>0时,y1与y2的大小.
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
题目内容
如图,一次函数y1=x+1的图像与反比例函数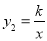 (k为常数,且k≠0)的图像都经过点A(m,2).
(k为常数,且k≠0)的图像都经过点A(m,2).
(1)求点A的坐标及反比例函数的表达式.
(2)结合图像直接比较:当x>0时,y1与y2的大小.

 阅读快车系列答案
阅读快车系列答案