题目内容
16.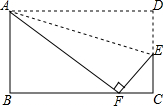 如图,将矩形ABCD沿直线AE折叠,顶点D恰好落在BC边上F处,CE=3,AB=8,AD=12,则BF=8.
如图,将矩形ABCD沿直线AE折叠,顶点D恰好落在BC边上F处,CE=3,AB=8,AD=12,则BF=8.
分析 由矩形的性质得出∠C=90°,CD=AB=8,BC=AD=12,得出DE=5,由折叠的性质得出EF=DE=5,在Rt△CEF中,由勾股定理求出CF,即可得出BF.
解答 解:∵四边形ABCD是矩形,
∴∠C=90°,CD=AB=8,BC=AD=12,
∵CE=3,
∴DE=8-3=5,
由折叠的性质得:EF=DE=5,
在Rt△CEF中,根据勾股定理得:CF=$\sqrt{E{F}^{2}-C{E}^{2}}$=$\sqrt{{5}^{2}-{3}^{2}}$=4,
∴BF=BC-CF=12-4=8;
故答案为:8.
点评 本题考查了矩形的性质、折叠的性质、勾股定理;熟练掌握矩形和翻折变换的性质,并能进行推理计算是解决问题的关键.

练习册系列答案
 教材全解字词句篇系列答案
教材全解字词句篇系列答案
相关题目
10.计算(-3)×2-1的结果是( )
| A. | -5 | B. | -7 | C. | 6 | D. | -6 |
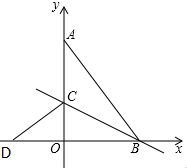 如图,在平面直角坐标系中,点A(0,8),B(6,0),连接AB,将△AOB沿过点B的直线折叠,使点A落在x轴上的点D处,折痕所在的直线交y轴正半轴于点C,则直线DC的解析式为y=$\frac{3}{4}$x+3.
如图,在平面直角坐标系中,点A(0,8),B(6,0),连接AB,将△AOB沿过点B的直线折叠,使点A落在x轴上的点D处,折痕所在的直线交y轴正半轴于点C,则直线DC的解析式为y=$\frac{3}{4}$x+3.
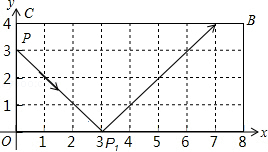 如图,弹性小球从点P(0,3)出发,沿所示方向运动,每当小球碰到矩形OABC的边时反弹,反弹时反射角等于入射角,当小球第1次碰到矩形的边时的点为P1,第2次碰到矩形的边时的点为P2,…,第n次碰到矩形的边时的点为Pn,则点P2015的坐标是( )
如图,弹性小球从点P(0,3)出发,沿所示方向运动,每当小球碰到矩形OABC的边时反弹,反弹时反射角等于入射角,当小球第1次碰到矩形的边时的点为P1,第2次碰到矩形的边时的点为P2,…,第n次碰到矩形的边时的点为Pn,则点P2015的坐标是( )