题目内容
学习三角形后,九(6)班的王老师给了这样一个题让同学们讨论:“已知一个三角形的两边长分别是6cm和5cm,其中一个内角是30°,求这个三角形的面积是多少?”于是得到很多结果:甲同学认为面积应该是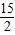 cm2,乙同学认为面积应该是
cm2,乙同学认为面积应该是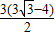 cm2而丙同学认为面积是
cm2而丙同学认为面积是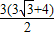 cm2等,你认为他们的说法全面吗?若你有不同结论,请你用你所学的数学知识求出其面积.
cm2等,你认为他们的说法全面吗?若你有不同结论,请你用你所学的数学知识求出其面积.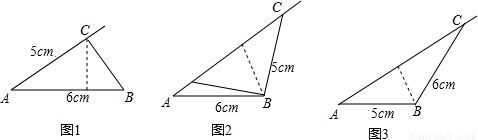
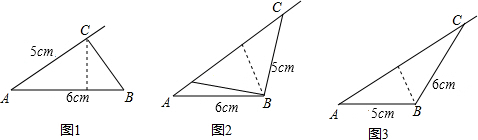
【答案】分析:分类讨论:①30°角的两邻边是6cm和5cm;②30°角的对边和邻边分别是6cm和5cm;③30°角的对边和邻边分别是5cm和6cm;④30°角的两邻边是5cm和6cm.
解答: 解:不全面,应该有四种情况.
解:不全面,应该有四种情况.
①如图①所示,
过C作CD⊥BC于D,
在Rt△ACD中,CD= AC=
AC= ,
,
∴S△ABC= AB•CD=
AB•CD= ×6cm×
×6cm× cm=
cm= cm2;
cm2;
②如图②所示:过点B作BD⊥AC于点D.
在Rt△ABD中,BD= AB=
AB= cm,AD=
cm,AD=
 cm;
cm;
在Rt△BDC中,CD= cm(勾股定理),
cm(勾股定理),
∴S△ABC= AC•BD=
AC•BD= ×(
×(
 +
+ )×
)× cm=
cm= cm2;
cm2;
③如图③所示,过点B作BD⊥AC于点D.
在Rt△ABD中,BD= AB=3cm,AD=3
AB=3cm,AD=3 cm;
cm;
在Rt△BDC中,CD=4cm(勾股定理),
∴S△ABC= AC•BD=
AC•BD= ×(3
×(3 +4)×3cm=
+4)×3cm= cm2;
cm2;
④如图④所示:设CD=xcm,则
在Rt△ACD中,AD= xcm;
xcm;
在Rt△BCD中,BD= cm,
cm,
∴AD+BD= x+
x+ =6,
=6,
解得,x= ,或x=
,或x= ,
,
∴S△ABC= AB•CD=
AB•CD= ×(
×( )×6cm=
)×6cm= cm2;
cm2;
或S△ABC= AB•CD=
AB•CD= ×(
×( )×6cm=
)×6cm= cm2;
cm2;
综上所述,该三角形的面积是: cm2;
cm2; cm2;
cm2; cm2;
cm2; cm2.
cm2.
点评:本题考查了三角形的面积,三角形中的勾股定理的运用以及含30度角的直角三角形.解答该题需要分类讨论.
解答:
 解:不全面,应该有四种情况.
解:不全面,应该有四种情况.①如图①所示,
过C作CD⊥BC于D,
在Rt△ACD中,CD=
 AC=
AC= ,
,∴S△ABC=
 AB•CD=
AB•CD= ×6cm×
×6cm× cm=
cm= cm2;
cm2;②如图②所示:过点B作BD⊥AC于点D.
在Rt△ABD中,BD=
 AB=
AB= cm,AD=
cm,AD=
 cm;
cm;在Rt△BDC中,CD=
 cm(勾股定理),
cm(勾股定理),∴S△ABC=
 AC•BD=
AC•BD= ×(
×(
 +
+ )×
)× cm=
cm= cm2;
cm2;③如图③所示,过点B作BD⊥AC于点D.
在Rt△ABD中,BD=
 AB=3cm,AD=3
AB=3cm,AD=3 cm;
cm;在Rt△BDC中,CD=4cm(勾股定理),
∴S△ABC=
 AC•BD=
AC•BD= ×(3
×(3 +4)×3cm=
+4)×3cm= cm2;
cm2;④如图④所示:设CD=xcm,则
在Rt△ACD中,AD=
 xcm;
xcm;在Rt△BCD中,BD=
 cm,
cm,∴AD+BD=
 x+
x+ =6,
=6,解得,x=
 ,或x=
,或x= ,
,∴S△ABC=
 AB•CD=
AB•CD= ×(
×( )×6cm=
)×6cm= cm2;
cm2;或S△ABC=
 AB•CD=
AB•CD= ×(
×( )×6cm=
)×6cm= cm2;
cm2;综上所述,该三角形的面积是:
 cm2;
cm2; cm2;
cm2; cm2;
cm2; cm2.
cm2.点评:本题考查了三角形的面积,三角形中的勾股定理的运用以及含30度角的直角三角形.解答该题需要分类讨论.

练习册系列答案
 优翼小帮手同步口算系列答案
优翼小帮手同步口算系列答案
相关题目
 cm2,乙同学认为面积应该是
cm2,乙同学认为面积应该是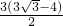 cm2而丙同学认为面积是
cm2而丙同学认为面积是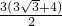 cm2等,你认为他们的说法全面吗?若你有不同结论,请你用你所学的数学知识求出其面积.
cm2等,你认为他们的说法全面吗?若你有不同结论,请你用你所学的数学知识求出其面积.