题目内容
【题目】如图，在Rt△ABC中，∠C=90°，AC=6，BC=8，点M在AC边上，点N从点C出发沿折线CB﹣BA运动到点A停止，点P是点C关于直线MN的对称点，连接MP，NP（当点N与点C，A重合时，点P均与点C重合）．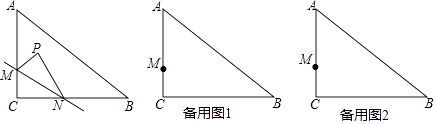
（1）若CM=2，
①又当点N在CB上，MP∥BC时，则CN= ， MN=；
（2）在（1）的条件下，求点P到AB边的距离的最小值，并求出当取得这个最小值时，点P运动路线的长是多少？（参考数据：sin54°=cos36°≈ 
，sin36°=cos54°≈ 
，结果保留π）
（3）设MC=a（a＞2），其他条件不变，当有且只能有唯一的点P落在线段AB上时，直接写出a的取值范围 ．
【答案】
（1）2,2 
②又当MN∥AB时,求CN的长；解：当MN∥AB时,△MNC∽△ABC,∴ 
,即 
,∴CN= 
（2）解：P在M为圆心，CM为半径的圆周上运动，
作MT⊥AB于T，如图2所示：
则PT=MT﹣2，当MT最小时，P在线段MT上最小，
∵AB= 
=10，sinA= 
= 
= 
，
∴MT= AM= （6﹣2）= 
，
∴PT= ﹣2= 
，
即点P到AB边的距离的最小值为 ；
∵cos∠AMT=sinA= ，
∴∠AMT=36°，
∴∠CMT=180°﹣36°=144°，
∴点P运动路线的长= 
= 
（3）a= 或3＜a≤6
【解析】解：（1）①连接CP，如图1所示：
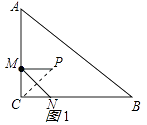
由对称的性质得：PM=CM=2，PC⊥MN，
∵MP∥BC，∠C=90°，
∴∠PMC=90°，
∴△PMC是等腰直角三角形，
∴∠PCM=45°，
∴∠PCN=90°﹣45°=45°，
∴∠CNM=45°，
∴△CMN是等腰直角三角形，
∴CN=CM=2，MN= CM=2 ；
所以答案是：2，2 ；
⑶分情况：①当圆M与AB相切时，sinA= 
，
解得：a= ；②当 ＜a≤3时，圆M与AB有2个交点；③当3＜a≤6时，圆M与线段AB仅1个交点；
综上所述：当a= 或3＜a≤6时，圆M与线段AB有1个交点；
即当有且只能有唯一的点P落在线段AB上时，a的取值范围是a= 或3＜a≤6；
所以答案是：a= 或3＜a≤6．
【考点精析】本题主要考查了直线与圆的三种位置关系的相关知识点，需要掌握直线与圆有三种位置关系：无公共点为相离；有两个公共点为相交,这条直线叫做圆的割线；圆与直线有唯一公共点为相切，这条直线叫做圆的切线，这个唯一的公共点叫做切点才能正确解答此题．
