题目内容
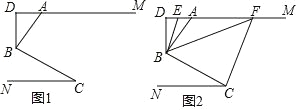
【题目】如图，已知AD⊥EF，CE⊥EF，∠2+∠3=180°．
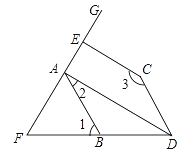
（1）请说明∠1=∠BDC；
（2）若∠1=70°，DA平分∠BDC，试求∠FAB的度数．
【答案】（1）见解析；（2）55°.
【解析】
(1)先根据垂直的定义得出∠GAD=∠GEC=90°，故可得出AD∥CE，再由平行线的性质∠ADC+∠3=180°，据此可得出AB∥CD，进而可得出结论；
(2)先根据平行线的性质得出∠BDC=∠1=70°，再由DA平分∠BDC得出∠ADC的度数，进而得出∠2的度数，由∠FAB=∠FAD-∠2即可得出结论．
(1)∵AD⊥EF，CE⊥EF，
∴∠GAD=∠GEC=90°，
∴AD∥CE，
∴∠ADC+∠3=180°，
又∵∠2+∠3=180°，
∴∠2=∠ADC，
∴AB∥CD，
∴∠1=∠BDC；
(2) ∵AD⊥EF，
∴∠FAD=90°，
∵AB∥CD，
∴∠BDC=∠1=70°，
∵DA平分∠BDC，
∴∠ADC=
∠BDC=×70°=35°，
∵AB∥CD，
∴∠2=∠ADC=35°，
∴∠FAB=∠FAD-∠2=90°-35°=55°．
练习册系列答案
相关题目
