题目内容
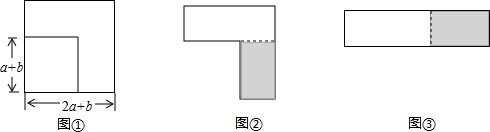
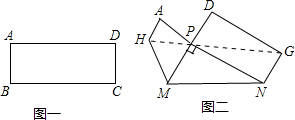
把图一的长方形纸片ABCD折叠,B、C两点恰好重合落在AD边上的点P处(如图二),已知∠MPN=90°,PM=3,PN=4,①求BC的长;②求长方形纸片ABCD的面积;③求图二中AD的长.

 解:①∵∠MPN=90°,PM=3,PN=4,
解:①∵∠MPN=90°,PM=3,PN=4,∴MN=5.
∴BC=MP+MN+NP=12.
②作PF⊥MN于F.
则AB=PF=
 =2.4.
=2.4.则长方形纸片ABCD的面积=AB•BC=28.8.
③根据折叠,知AP=DP=AB=2.4.
根据勾股定理,得
AD=
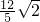 .
.分析:①根据折叠的性质,得BC的长即为MP+MN+NP的长,根据勾股定理求得MN的长即可;
②要求长方形的面积,在①的基础上,关键是求得AB的长,即等于直角三角形MPN斜边上的高,即为直角三角形两条直角边的乘积除以斜边;
③根据折叠,知AP=DP=AB,再根据勾股定理进行计算.
点评:此题综合运用了折叠的性质、勾股定理以及直角三角形的面积公式.

练习册系列答案
相关题目
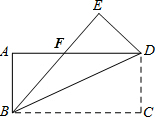 如图,把一张长方形纸片ABCD沿对角线BD折叠,使C点落在E处,BE与AD相交于点F,下列结论:
如图,把一张长方形纸片ABCD沿对角线BD折叠,使C点落在E处,BE与AD相交于点F,下列结论: 把一张长方形纸片ABCD对折后展开到如图所示的位置,其中EF是折痕,则图中EF垂直的线段共有
把一张长方形纸片ABCD对折后展开到如图所示的位置,其中EF是折痕,则图中EF垂直的线段共有