化简($\frac{a+2}{{a}^{2}-2a}$-$\frac{a-1}{{a}^{2}-4a+4}$)÷$\frac{4-a}{{a}^{2}-2a}$.并在0.1.2.3.4中选一个你喜欢的数作为a的值求原式的值．题目和参考答案——青夏教育精英家教网—

题目内容

6．化简（$\frac{a+2}{{a}^{2}-2a}$-$\frac{a-1}{{a}^{2}-4a+4}$）÷$\frac{4-a}{{a}^{2}-2a}$，并在0，1，2，3，4中选一个你喜欢的数作为a的值求原式的值．

分析先根据分式混合运算的法则把原式进行化简，再选取a的值代入进行计算即可．

解答解：原式=（$\frac{a+2}{a（a-2）}$-$\frac{a-1}{（a-2）^{2}}$）•$\frac{a（a-2）}{4-a}$
=$\frac{a-4}{a（a-2）^{2}}$•$\frac{a（a-2）}{4-a}$
=$\frac{1}{2-a}$，
当a=1时，原式=1．

点评本题考查的是分式的化简求值，熟知分式混合运算的法则是解答此题的关键．

练习册系列答案

150加50篇英语完形填空与阅读理解系列答案

17．已知a²+b²+4a+5=2b，求$\frac{a+b}{a-b}$的值．

14．已知x²-（m-1）xy+49y²是一个完全平方式，求m的值．

1．要配置15%的硝酸溶液240千克，需用8%和50%的硝酸溶液的克数分别（　　）

11．先阅读第（1）小题的解题过程，再解答第（2）小题．
（1）已知a²-3a+1=0，求a²+$\frac{1}{{a}^{2}}$的值．
解：由a²-3a+1=0知a≠0，
等式两边同除以a，得
∴a-3+$\frac{1}{a}$=0，即a+$\frac{1}{a}$=3
∴a²+$\frac{1}{{a}^{2}}$=$（a+\frac{1}{a}）^{2}$-2=7；
（2）已知：y²+3y-1=0，求y⁴+$\frac{1}{{y}^{4}}$的值．

18．已知函数自变量的取值范围是$\frac{1}{3}$＜x≤1，那么这个函数的解析式可能是（　　）

A．

y=$\frac{1-x}{\sqrt{3x-1}}$

B．

y=$\sqrt{\frac{1-x}{3x-1}}$

C．

y=$\frac{\sqrt{3x-1}}{1-x}$

D．

y=$\frac{1}{\sqrt{1-x}}$-$\sqrt{3x-1}$

15．

已知：平行四边形ABCD中，AB=2BC，延长CB到E，BE=BC，延长BC到F，CF=BC，AF、DE相交于G，求证：AF⊥DE．

19．

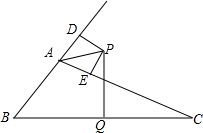如图，△ABC的外角∠DAC的平分线交BC边的垂直平分线于P点，PD⊥AB于D，PE⊥AC于E．
（1）求证：BD=CE；
（2）若AB=6cm，AC=10cm，求AD的长．

试题分类