题目内容
3.某村计划对总长为1800m的道路进行改造,安排甲、乙两个工程队完成.已知甲队每天能完成的道路长度是乙队每天能完成的2倍,并且在独立完成长为400m的道路时,甲队比乙队少用4天.(1)求甲、乙两工程队每天能完成道路的长度分别是多少m?
(2)若村委每天需付给甲队的道路改造费用为0.4万元,乙队为0.25万元,要使这次的道路改造费用不超过8万元,至少应安排甲队工作多少天?
分析 (1)设乙工程队每天能完成道路的长度是xm,根据在独立完成400m道路的长度时,甲队比乙队少用4天,列出方程,求解即可;
(2)设应安排甲队工作y天,根据这次的修路总费用不超过8万元,列出不等式,求解即可.
解答 解:(1)设乙工程队每天能完成道路的长度是xm,根据题意得:
$\frac{400}{x}$-$\frac{400}{2x}$=4,
解得:x=50,
经检验x=50是原方程的解,
则甲工程队每天能完成道路的长度是50×2=100m.
答:甲工程队每天能完成道路的长度是100m,乙工程队每天能完成道路的长度是50m.
(2)设应安排甲队工作y天,根据题意得:
0.4y+$\frac{1800-100y}{50}$×0.25≤8,
解得:y≥10.
答:至少应安排甲队修建10天.
点评 此题考查了分式方程的应用和一元一次不等式的应用;关键是分析题意,找到合适的数量关系列出方程和不等式,解分式方程时要注意检验.

练习册系列答案
相关题目
14.下列说法正确的是( )
| A. | 2是4的一个平方根 | B. | -4的平方根是±2 | ||
| C. | 4的平方根是2 | D. | (-2)2的算术平方根是-2 |
13.《孙子算经》中有一道题,原文是:“今有木,不知长短.引绳度之,余绳四尺五寸;屈绳量之,不足一尺.木长几何?”意思是:用一根绳子去量一根长木,绳子还剩余4.5尺;将绳子对折再量长木,长木还剩余1尺,问木长多少尺.设木长为x尺,绳子长为y尺,则下列符合题意的方程组是( )
| A. | $\left\{\begin{array}{l}{y=x+4.5}\\{\frac{1}{2}y=x+1}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{y=x+4.5}\\{\frac{1}{2}y=x-1}\end{array}\right.$ | C. | $\left\{\begin{array}{l}{y=4.5-x}\\{\frac{1}{2}y=x+1}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{y=x-4.5}\\{\frac{1}{2}y=x-1}\end{array}\right.$ |
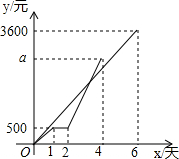 甲、乙两专卖店某段时间内销售收入y(元)与天数x(天)的函数图象如图,在这期间乙专卖店因故停业一天,重新开业后,乙专卖店的日均销售收入是原来的2倍,请解决下列问题:
甲、乙两专卖店某段时间内销售收入y(元)与天数x(天)的函数图象如图,在这期间乙专卖店因故停业一天,重新开业后,乙专卖店的日均销售收入是原来的2倍,请解决下列问题: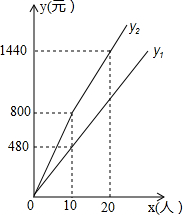 某景区门票价格80元/人,景区为吸引游客,对门票价格进行动态管理,非节假日打a折,节假日期间,10人以下(包括10人)不打折,10人以上超过10人的部分打b折,设游客为x人,门票费用为y元,非节假日门票费用y1(元)及节假日门票费用y2(元)与游客x(人)之间的函数关系如图所示.
某景区门票价格80元/人,景区为吸引游客,对门票价格进行动态管理,非节假日打a折,节假日期间,10人以下(包括10人)不打折,10人以上超过10人的部分打b折,设游客为x人,门票费用为y元,非节假日门票费用y1(元)及节假日门票费用y2(元)与游客x(人)之间的函数关系如图所示.