Question

【题目】在学习了数轴后，小亮决定对数轴进行变化应用：

（1）应用一：已知点A在数轴上表示为，数轴上任意一点B表示的数为，则AB两点的距离可以表示为 ；应用这个知识，请写出当 时，有最小值为 .

（2）应用二：从数轴上取下一个单位长度的线段，第一次剪掉原长的，第二次剪掉剩下的，依次类推，每次都剪掉剩下的，则剪掉5次后剩下线段长度为 ；应用这个原理，请计算：.

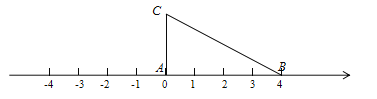
（3）应用三：如图，将一根拉直的细线看作数轴，一个三边长分别为的三角形的顶点与原点重合，边在数轴正半轴上，将数轴正半轴的线沿的顺序依次缠绕在三角形的边上，负半轴的线沿的顺序依次缠绕在三角形的边上.

①如果正半轴的线缠绕了5圈，负半轴的线缠绕了3圈，求绕在点上的所有数之和；

②如果正半轴的线不变，将负半轴的线拉长一倍，即原线上的点的位置对应着拉长后的数，并将三角形向正半轴平移一个单位后再开始绕，求绕在点且绝对值不超过100的所有数之和.

Answer 1

【答案】（1） （2）（3）①②

【解析】

（1）根据数轴上两点间的距离的表示列出式子即可；
（2）第1次剪掉的长度是；第1次剪掉后剩下的长度是

第2次剪掉的长度是 第2次剪掉后剩下的长度是

第3次剪掉的长度是；第3次剪掉后剩下的长度是…由此规律得出：第7次剪掉后剩下的长度是；即可求出.

（3）①分别找出正半轴以及负半轴在点上的数字之间的规律，即可求出所有数字之和.

②绕在点且绝对值不超过100的所有数,求和即可.

（1）已知点A在数轴上表示为，数轴上任意一点B表示的数为，则AB两点的距离可以表示为应用这个知识，当 时，有最小值为8.

故答案为：

（2）第1次剪掉的长度是；第1次剪掉后剩下的长度是

第2次剪掉的长度是 第2次剪掉后剩下的长度是

第3次剪掉的长度是；第3次剪掉后剩下的长度是…由此规律得出第5次剪掉剩下的长度是，…第7次剪掉后剩下的长度是；

所以第5次剪掉剩下的长度是

则

（3）①如果正半轴的线缠绕了5圈，绕在点C的数字分别为：

负半轴的线缠绕了3圈，绕在点上的数字分别为：

则绕在点上的所有数之和为：

②如果正半轴的线不变，并将三角形向正半轴平移一个单位后再开始绕，则正半轴上绕在点且绝对值不超过100的数字有：

将负半轴的线拉长一倍，并将三角形向正半轴平移一个单位后再开始绕，正半轴上绕在点且绝对值不超过100的数字有：

绕在点且绝对值不超过100的所有数之和为：