题目内容

如图，B是线段AD上一动点，沿A至D的方向以2cm/s的速度运动，C是线段BD的中点，AD=10cm.设点B运动的时间为t s.

（1）当t=2 s时，①AB= cm;

②求线段CD的长度.

（2）在运动过程中，若线段AB的中点为E，则EC的长是否变化？若不变。求出EC的长；若发生变化，请说明理由。

（1）①A=4cm ; ②CD=3cm；（2）不变，EC=5cm，理由详见解析. 【解析】试题分析：（1）①根据AB=2t即可得出结论；②先求出BD的长，再根据C是线段BD的中点即可得出CD的长； （2）直接根据中点公式即可得出结论． 试题解析：【解析】 （1）①∵B是线段AD上一动点，沿A至D以2cm/s的速度运动，∴当t=2时，AB=2×2=4cm． ②∵AD=10c...
练习册系列答案
相关题目

下图是某儿童乐园为小朋友设计的滑梯平面图.已知BC=4 m,AB=6 m,中间平台宽度DE=1 m,EN,DM,CB为三根垂直于AB的支柱,垂足分别为N,M,B,∠EAB=31°,DF⊥BC于点F,∠CDF=45°,求DM和BC的水平距离BM的长度.(结果精确到0.1 m.参考数据:sin 31°≈0.52,cos 31°≈0.86,tan 31°≈0.60)

2.5m. 【解析】试题分析：设DF=x，在Rt△DFC中，可得CF=DF=x，则BF=4-x，根据线段的和差可得AN=5-x，EN=DM=BF=4－，在Rt△ANE中，∠EAB=，利用∠EAB的正切值解得x的值． 试题解析：【解析】 设DF=，在Rt△DFC中，∠CDF=， ∴CF=tan·DF=， 又∵CB=4， ∴BF=4－， ∵AB=6，DE=1，BM...

如图，在铁路旁有一李庄O，现要建一火车站，为了使李庄人乘车最方便，请你在铁路线上选一点来建火车站，应建在(　 　)

A. A点 B. B点 C. C点 D. D点

A 【解析】试题解析：根据垂线段最短可得：应建在A处， 故选A.

已知点P的坐标是（2，﹣3），那么点P关于原点的对称点P1的坐标是_____．

（2，﹣3） 【解析】试题解析：∵点P的坐标是（2，﹣3）， ∴点P关于原点的对称点P1的坐标是（﹣2，3）． 故答案为：（﹣2，3），

将抛物线y=2（x+1）2﹣2的图象先向左平移1个单位长度，再向上平移3个单位长度，则顶点坐标为（　　）

A. （﹣2，1） B. （2，1） C. （0，1） D. （﹣2，﹣5）

A 【解析】试题解析：y=2（x+1）2﹣2的图象先向左平移1个单位长度，再向上平移3个单位长度，得 y=2（x+2）2+1， 顶点坐标为（﹣2，1）， 故选A．

解下列方程:

（1）；（2） .

（1）x=;（2）x=. 【解析】试题分析：（1）去括号，移项，合并同类项，系数化为1即可得解； （2）去分母，去括号，移项，合并同类项，系数化为1即可得解． 试题解析：（1）去括号得：3x-3-x=1-2x+1 移项得：3x-x+2x=1+1+3 合并同类项得：4x=5 化系数为1：x= （2）去分母得： 去括号得：2x-2-x-2=12-3x+6...

如果实数a，b满足（a-3）2+|b+1|=0，那么= 。

-1 【解析】【解析】 由题意得：a-3=0，b+1=0，解得：a=3，b=-1，∴ =-1．故答案为：-1．

在一节数学实践活动课上，老师拿出三个边长都为5cm的正方形硬纸板，他向同学们提出了这样一个问题：若将三个正方形纸板不重叠地放在桌面上，用一个圆形硬纸板将其盖住，这样的圆形硬纸板的最小直径应有多大？问题提出后，同学们经过讨论，大家觉得本题实际上就是求将三个正方形硬纸板无重叠地适当放置，圆形硬纸板能盖住时的最小直径．老师将同学们讨论过程中探索出的三种不同摆放类型的图形画在黑板上，如下图所示：

（1）计算（结果保留根号与π）．

（Ⅰ）图①能盖住三个正方形所需的圆形硬纸板最小直径应为 cm；

（Ⅱ）图②能盖住三个正方形所需的圆形硬纸板最小直径为 cm；

（Ⅲ）图③能盖住三个正方形所需的圆形硬纸板最小直径为 cm；

（2）其实上面三种放置方法所需的圆形硬纸板的直径都不是最小的，请你画出用圆形硬纸板盖住三个正方形时直径最小的放置方法，（只要画出示意图，不要求说明理由），并求出此时圆形硬纸板的直径．

（1）（Ⅰ）5cm；（Ⅱ）10cm；（Ⅲ）10cm；（2）直径为. 【解析】试题分析：（1）（Ⅰ）观察图形可知：图①能盖住三个正方形所需的圆形硬纸板最小直径=三个正方形组成的矩形的对角线长，利用勾股定理可求出结果；（Ⅱ）图②中圆形硬纸板的半径是正方形的对角线长，利用勾股定理可求出结果；（Ⅲ）图③中圆形硬纸板的直径是正方形的对角线长的2倍，利用勾股定理可求出结果；（2）把三个正方形摆成“品”字...

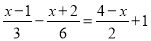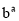已知点和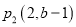关于原点对称，则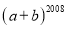的值为（ ）

A. 1 B. 0 C. -1 D.

A 【解析】试题解析：根据题意得：a-1=-2，b-1=-1， 解得：a=-1 b=0． 则（a+b）2008=1． 故选A．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网