题目内容
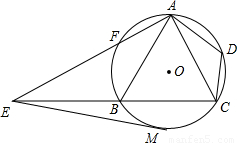
如图,已知四边形ABCD内接于⊙O,A是 的中点,AE⊥AC于A,与⊙O及CB的延长线分别交于点F、E,且
的中点,AE⊥AC于A,与⊙O及CB的延长线分别交于点F、E,且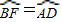 ,EM切⊙O于M.
,EM切⊙O于M.(1)求证:△ADC∽△EBA;
(2)求证:AC2=
 BC•CE;
BC•CE;(3)如果AB=2,EM=3,求cot∠CAD的值.
【答案】分析:(1)欲证(1)△ADC∽△EBA,只要证明两个角对应相等就可以.可以转化为证明 就可以;
就可以;
(2)过A作AH⊥BC于H,根据射影定理就可以得到结论.
(3)A是 中点,则AC=AB=2,根据切割线定理,以及△CAD∽△ABE就可以求的结论.
中点,则AC=AB=2,根据切割线定理,以及△CAD∽△ABE就可以求的结论.
解答: (1)证明:∵四边形ABCD内接于⊙O,
(1)证明:∵四边形ABCD内接于⊙O,
∴∠CDA=∠ABE.
∵ ,
,
∴∠DCA=∠BAE.
∴△ADC∽△EBA;
(2)证明:过A作AH⊥BC于H(如图),
∵A是 中点,
中点,
∴AB=AC,
又∵AH⊥BC于H,
∴HC=HB= BC,
BC,
∵∠CAE=90°,
∵AH⊥BC,
∴∠AHC=∠AHB=90°,
∴△ACH∽△AEC,
∴ =
= ,即AC2=HC•CE,
,即AC2=HC•CE,
又∵BC=2CH,
∴AC2=CH•CE= BC•CE;
BC•CE;
(3)解:∵A是 中点,AB=2,
中点,AB=2,
∴AC=AB=2.
∵EM是⊙O的切线,
∴EB•EC=EM2①
∵AC2= BC•CE,BC•CE=8 ②
BC•CE,BC•CE=8 ②
联立①②得:EC(EB+BC)=17.
∴EC2=17.
∵EC2=AC2+AE2,∴AE= ,
,
∵△CAD∽△ABE,
∴∠CAD=∠AEC.
∴cot∠CAD=cot∠AEC= .
.
点评:本题主要考查了三角形相似的判定方法,切割线定理及勾股定理的综合运用.
 就可以;
就可以;(2)过A作AH⊥BC于H,根据射影定理就可以得到结论.
(3)A是
 中点,则AC=AB=2,根据切割线定理,以及△CAD∽△ABE就可以求的结论.
中点,则AC=AB=2,根据切割线定理,以及△CAD∽△ABE就可以求的结论.解答:
 (1)证明:∵四边形ABCD内接于⊙O,
(1)证明:∵四边形ABCD内接于⊙O,∴∠CDA=∠ABE.
∵
 ,
,∴∠DCA=∠BAE.
∴△ADC∽△EBA;
(2)证明:过A作AH⊥BC于H(如图),
∵A是
 中点,
中点,∴AB=AC,
又∵AH⊥BC于H,
∴HC=HB=
 BC,
BC,∵∠CAE=90°,
∵AH⊥BC,
∴∠AHC=∠AHB=90°,
∴△ACH∽△AEC,
∴
 =
= ,即AC2=HC•CE,
,即AC2=HC•CE,又∵BC=2CH,
∴AC2=CH•CE=
 BC•CE;
BC•CE;(3)解:∵A是
 中点,AB=2,
中点,AB=2,∴AC=AB=2.
∵EM是⊙O的切线,
∴EB•EC=EM2①
∵AC2=
 BC•CE,BC•CE=8 ②
BC•CE,BC•CE=8 ②联立①②得:EC(EB+BC)=17.
∴EC2=17.
∵EC2=AC2+AE2,∴AE=
 ,
,∵△CAD∽△ABE,
∴∠CAD=∠AEC.
∴cot∠CAD=cot∠AEC=
 .
.点评:本题主要考查了三角形相似的判定方法,切割线定理及勾股定理的综合运用.

练习册系列答案
相关题目
 15、如图,已知四边形ABCD是等腰梯形,AB=DC,AD∥BC,PB=PC.求证:PA=PD.
15、如图,已知四边形ABCD是等腰梯形,AB=DC,AD∥BC,PB=PC.求证:PA=PD.
 的延长线分别交于点F、E,且
的延长线分别交于点F、E,且 (2013•梧州)如图,已知:AB∥CD,BE⊥AD,垂足为点E,CF⊥AD,垂足为点F,并且AE=DF.
(2013•梧州)如图,已知:AB∥CD,BE⊥AD,垂足为点E,CF⊥AD,垂足为点F,并且AE=DF.
