题目内容
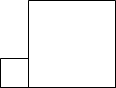 如图,要将边长为1,3的两个连接的正方形纸片,通过适当的剪拼,得到一个与之面积相等的正方形.
如图,要将边长为1,3的两个连接的正方形纸片,通过适当的剪拼,得到一个与之面积相等的正方形.
(Ⅰ)该正方形的边长为________(结果保留根号).
(Ⅱ)现要求只能用两条裁剪线,请你设计一种裁剪的方法,在图中画出裁剪线,并简要说明拼接的过程.

分析:(1)根据正方形的面积求出正方形边长即可;
(2)根据(1)中所求,首先在正方形中裁剪出两条长度为
 的边长,进而通过旋转的到即可.
的边长,进而通过旋转的到即可.解答:
 解:(Ⅰ)∵将边长为1,3的两个连接的正方形纸片,通过适当的剪拼,得到一个与之面积相等的正方形,
解:(Ⅰ)∵将边长为1,3的两个连接的正方形纸片,通过适当的剪拼,得到一个与之面积相等的正方形,∴新的正方形面积为10,
∴该正方形的边长为
 ;
;(Ⅱ)如图,过点B作 BC=3,画出两条裁剪线AC、CE.
把△ABC绕点A逆时针旋转90°得到△APG;
把△CDE绕点E顺时针旋转90°得到△GFE.此时,得到的四边形ACEG即为所求.
故答案为:
 .
.点评:此题主要考查了图形的剪拼,得出正方形的边长后利用旋转得出是解题关键.

练习册系列答案
 全优点练单元计划系列答案
全优点练单元计划系列答案
相关题目
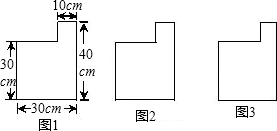
 (2013•西青区二模)如图,要将边长为1,3的两个连接的正方形纸片,通过适当的剪拼,得到一个与之面积相等的正方形.
(2013•西青区二模)如图,要将边长为1,3的两个连接的正方形纸片,通过适当的剪拼,得到一个与之面积相等的正方形.