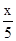题目内容
“数学建模”
(1)模型--小马喝水问题:直线MN表示一条河流的岸,在河流同侧有A、B两地,小马从A地出发到B地,中间要在河边饮水一次,请在图①中用直尺和圆规作出使小马行走最短路程的饮水点P的位置.(作在答题纸上,保留作图痕迹,并用黑水笔将痕迹描深)
(2)运用--和最小问题:如图②,E是边长为8的正方形ABCD边BC上一点,CE=2,P是对角线BD上的一个动点,求PC+PE的最小值.
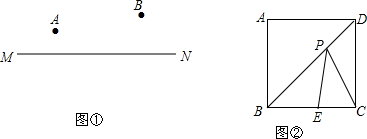
(1)模型--小马喝水问题:直线MN表示一条河流的岸,在河流同侧有A、B两地,小马从A地出发到B地,中间要在河边饮水一次,请在图①中用直尺和圆规作出使小马行走最短路程的饮水点P的位置.(作在答题纸上,保留作图痕迹,并用黑水笔将痕迹描深)
(2)运用--和最小问题:如图②,E是边长为8的正方形ABCD边BC上一点,CE=2,P是对角线BD上的一个动点,求PC+PE的最小值.
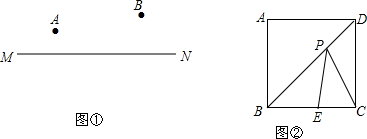
分析:(1)作点A关于直线l的对称点A′.连接A′B交直线l于点P,则点P即为所求点;
(2)连接AE,因为四边形ABCD是正方形,所以A、C两点关于直线BD对称,所以AE即为PC+PE的最小值,根据勾股定理即可得出AE的长.
(2)连接AE,因为四边形ABCD是正方形,所以A、C两点关于直线BD对称,所以AE即为PC+PE的最小值,根据勾股定理即可得出AE的长.
解答: 解:(1)如图①所示,点P即为所求点;
解:(1)如图①所示,点P即为所求点;
(2)如图②所示:
∵四边形ABCD是正方形,
BC=8,CE=2,
∴BE=6,
∴AE=
=
=10.
 解:(1)如图①所示,点P即为所求点;
解:(1)如图①所示,点P即为所求点;(2)如图②所示:
∵四边形ABCD是正方形,
BC=8,CE=2,
∴BE=6,
∴AE=
| AB2+BE2 |
| 82+62 |
点评:本题考查的是轴对称-最短路线问题,熟知“两点之间线段最短”是解答此题的关键.

练习册系列答案
 期末宝典单元检测分类复习卷系列答案
期末宝典单元检测分类复习卷系列答案
相关题目
春节期间某水库养殖场为适应市场需求,连续用20天时间,采用每天降低水位以减少捕捞成本的办法,对水库中某种鲜鱼进行捕捞、销售.九(1)班数学建模兴趣小组根据调查,整理出第x天(1≤x≤20且x为整数)的捕捞与销售的相关信息如表:
(1)在此期间该养殖场每天的捕捞量与前一天末的捕捞量相比是如何变化的?
(2)假定该养殖场每天捕捞和销售的鲜鱼没有损失,且能在当天全部售出,求第x天的收入y(元)与x(天)之间的函数关系式?(当天收入=日销售额-日捕捞成本)
(3)试说明(2)中的函数y随x的变化情况,并指出在第几天y取得最大值,最大值是多少?
| 鲜鱼销售单价(元/kg) | 20 | ||
| 单位捕捞成本(元/kg) | 5-
| ||
| 捕捞量(kg) | 950-10x |
(2)假定该养殖场每天捕捞和销售的鲜鱼没有损失,且能在当天全部售出,求第x天的收入y(元)与x(天)之间的函数关系式?(当天收入=日销售额-日捕捞成本)
(3)试说明(2)中的函数y随x的变化情况,并指出在第几天y取得最大值,最大值是多少?
春节期间某水库养殖场为适应市场需求,连续用20天时间,采用每天降低水位以减少捕捞成本的办法,对水库中某种鲜鱼进行捕捞、销售.九(1)班数学建模兴趣小组根据调查,整理出第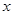 天(
天(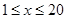 且
且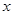 为整数)的捕捞与销售的相关信息如表:
为整数)的捕捞与销售的相关信息如表:
| 鲜鱼销售单价(元/kg) | 20 |
| 单位捕捞成本(元/kg) | 5-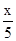 |
| 捕捞量(kg) | 950-10x |
(2)假定该养殖场每天捕捞和销售的鲜鱼没有损失,且能在当天全部售出,求第
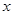 天的收入
天的收入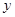 (元)与
(元)与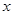 (天)之间的函数关系式?(当天收入=日销售额—日捕捞成本)
(天)之间的函数关系式?(当天收入=日销售额—日捕捞成本)(3)试说明⑵中的函数
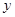 随
随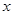 的变化情况,并指出在第几天
的变化情况,并指出在第几天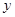 取得最大值,最大值是多少?
取得最大值,最大值是多少? 中秋节期间某水库养殖场为适应市场需求,连续用20天时间,采用每天降低水位以减少捕捞成本的办法,对水库中某种鲜鱼进行捕捞、销售.
九(1)班数学建模兴趣小组根据调查,整理出第x天( )的捕捞与销售的相关信息如下:
)的捕捞与销售的相关信息如下:
|
鲜鱼销售单价(元/kg) |
20 |
|
单位捕捞成本(元/kg) |
|
|
捕捞量(kg) |
950-10x |
(1)在此期间该养殖场每天的捕捞量与前一天的捕捞量相比是如何变化的?
(2)假定该养殖场每天捕捞和销售的鲜鱼没有损失,且能在当天全部售出,求第x天的收入y(元)与x(元)之间的函数关系式;(当天收入=日销售额 日捕捞成本)
日捕捞成本)
(3)试说明(2)中的函数y随x的变化情况,并指出在第几天y取得最大值,最大值是多少?
春节期间某水库养殖场为适应市场需求,连续用20天时间,采用每天降低水位以减少捕捞成本的办法,对水库中某种鲜鱼进行捕捞、销售.九(1)班数学建模兴趣小组根据调查,整理出第 天(
天(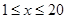 且
且 为整数)的捕捞与销售的相关信息如表:
为整数)的捕捞与销售的相关信息如表:
|
鲜鱼销售单价(元/kg) |
20 |
|
单位捕捞成本(元/kg) |
5- |
|
捕捞量(kg) |
950-10x |
(1)在此期间该养殖场每天的捕捞量与前一天的捕捞量相比是如何变化的 (填“增加”或“减少”了多少kg.)
(2)假定该养殖场每天捕捞和销售的鲜鱼没有损失,且能在当天全部售出,求第 天的收入
天的收入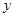 (元)与
(元)与 (天)之间的函数关系式?(当天收入=日销售额—日捕捞成本)
(天)之间的函数关系式?(当天收入=日销售额—日捕捞成本)
(3)试说明⑵中的函数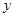 随
随 的变化情况,并指出在第几天
的变化情况,并指出在第几天 取得最大值,最大值是多少?
取得最大值,最大值是多少?